早教吧作业答案频道 -->数学-->
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动
题目详情
如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的 P与AB、OA的另一个交点分别为C、D,连结CD、QC.
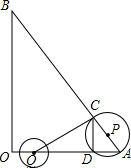
(1)当t为何值时,点Q与点D重合?
(2)当 Q经过点A时,求 P被OB截得的弦长.
(3)若 P与线段QC只有一个公共点,求t的取值范围.

(1)当t为何值时,点Q与点D重合?
(2)当 Q经过点A时,求 P被OB截得的弦长.
(3)若 P与线段QC只有一个公共点,求t的取值范围.
▼优质解答
答案和解析
(1)∵OA=6,OB=8,
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是 P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴
=
,
∴AD=
t,
当Q与D重合时,
AD+OQ=OA,
∴
t+t=6,
∴t=
;
(2)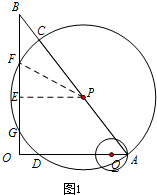 当 Q经过A点时,如图1,
当 Q经过A点时,如图1,
OQ=OA-QA=4,
∴t=
=4s,
∴PA=4,
∴BP=AB-PA=6,
过点P作PE⊥OB于点E, P与OB相交于点F、G,
连接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴
=
,
∴PE=
,
∴由勾股定理可求得:EF=
,
由垂径定理可求知:FG=2EF=
;
(3)当QC与 P相切时,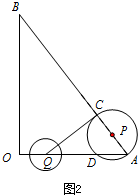 如图2,
如图2,
此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6-t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴
=
,
∴
=
,
∴t=
,
∴当0<t≤
时, P与QC只有一个交点,
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=
,
∴当
<t≤5时, P与QC只有一个交点,
综上所述,当, P与QC只有一个交点,t的取值范围为:0<t≤
或
<t≤5.
∴由勾股定理可求得:AB=10,
由题意知:OQ=AP=t,
∴AC=2t,
∵AC是 P的直径,
∴∠CDA=90°,
∴CD∥OB,
∴△ACD∽△ABO,
∴
| AC |
| AB |
| AD |
| OA |
∴AD=
| 6 |
| 5 |
当Q与D重合时,
AD+OQ=OA,
∴
| 6 |
| 5 |
∴t=
| 30 |
| 11 |
(2)
 当 Q经过A点时,如图1,
当 Q经过A点时,如图1,OQ=OA-QA=4,
∴t=
| 4 |
| 1 |
∴PA=4,
∴BP=AB-PA=6,
过点P作PE⊥OB于点E, P与OB相交于点F、G,
连接PF,
∴PE∥OA,
∴△PEB∽△AOB,
∴
| PE |
| OA |
| BP |
| AB |
∴PE=
| 18 |
| 5 |
∴由勾股定理可求得:EF=
2
| ||
| 5 |
由垂径定理可求知:FG=2EF=
4
| ||
| 5 |
(3)当QC与 P相切时,
 如图2,
如图2,此时∠QCA=90°,
∵OQ=AP=t,
∴AQ=6-t,AC=2t,
∵∠A=∠A,
∠QCA=∠ABO,
∴△AQC∽△ABO,
∴
| AQ |
| AB |
| AC |
| OA |
∴
| 6-t |
| 10 |
| 2t |
| 6 |
∴t=
| 18 |
| 13 |
∴当0<t≤
| 18 |
| 13 |
当QC⊥OA时,
此时Q与D重合,
由(1)可知:t=
| 30 |
| 11 |
∴当
| 30 |
| 11 |
综上所述,当, P与QC只有一个交点,t的取值范围为:0<t≤
| 18 |
| 13 |
| 30 |
| 11 |
看了 如图,在△AOB中,∠AOB...的网友还看了以下:
已知双曲线C的焦点在x轴上,一条渐近线的倾斜角为60度,双曲线过点(1,根号2),直线l:y=a 2020-05-13 …
在平面直角坐标系XOY中,Y=根号三被圆C1:X^2+Y^2+8X+F=0截得弦长为21求圆C1的 2020-06-09 …
在平面直角坐标系内,设M(x1,y1)、N(x2,y2)为不同的两点,直线l的方程为ax+by+c 2020-06-20 …
如图,M为半圆形导线框,圆心为OM;N是圆心角为直角的扇形导线框,圆心为ON;两导线框在同一竖直面 2020-07-24 …
如图,M为半圆形导线框,圆心为OM;N是圆心角为直角的扇形导线框,圆心为ON;两导线框在同一竖直面 2020-07-24 …
已知圆心为C的圆经过点A(-3,0)和B(1,0),且圆心C在直线Y=x+1上.求圆C的标准方程. 2020-07-26 …
如图所示,以O为圆心、MN为直径的圆的左半部分内有垂直纸面向里的匀强磁场,三个不计重力、质量相同、带 2020-11-01 …
(2010·山东卷)25.(18分)如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场 2020-12-05 …
已知椭圆x2a2+y2b21的焦距为4,且与椭圆x2+y2\2=1有相同的离心率,斜率为k的直线l经 2021-01-11 …
已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为4,离心率为22,斜率为k的直线l经过点M( 2021-01-13 …