早教吧作业答案频道 -->数学-->
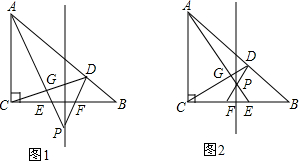
在Rt△ABC中,∠ACB=90°,AC=BC,P是BC中垂线l上一动点,连接PA,交CB于点E,F是点E关于l的对称点.将PF延长交AB于点D,连接CD交PA于点G.(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD
题目详情
在Rt△ABC中,∠ACB=90°,AC=BC,P是BC中垂线l上一动点,连接PA,交CB于点E,F是点E关于l的对称点.将PF延长交AB于点D,连接CD交PA于点G.
(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD⊥AE;
(2)如图,若点P移动到BC的上方时,其他条件不变,请试写出线段AE、CD、DF的数量关系,并加以证明.
(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD⊥AE;
(2)如图,若点P移动到BC的上方时,其他条件不变,请试写出线段AE、CD、DF的数量关系,并加以证明.

▼优质解答
答案和解析
(2)证明:如图1,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°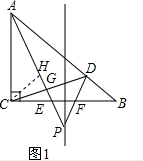
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,
∴∠AEC=∠BFD,
在△CEH与△BFD中,
,
∴△CEH≌△BFD(ASA).
∴CH=BD,
在△ACH与△CBD中,
,
∴△ACH≌△CBD
∴∠BCD=∠CAH,
∵∠CAE+∠CEA=90°
∴∠GCE+∠CEG=90°
∴∠CGH=90°
∴CD⊥AE;
(2)AE=CD+DF,
证明:如图2,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,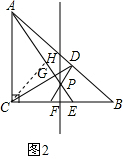
∴∠AEC=∠BFD,
在△CEH与△BFD中,
,
∴△CEH≌△BFD(ASA).
∴EH=FD,
在△ACH与△CBD中,
,
∴△ACH≌△CBD,
∴AH=CD,
∵AE=AH+EH,
∴AE=CD+DF.
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°

又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,
∴∠AEC=∠BFD,
在△CEH与△BFD中,
|
∴△CEH≌△BFD(ASA).
∴CH=BD,
在△ACH与△CBD中,
|
∴△ACH≌△CBD
∴∠BCD=∠CAH,
∵∠CAE+∠CEA=90°
∴∠GCE+∠CEG=90°
∴∠CGH=90°
∴CD⊥AE;
(2)AE=CD+DF,
证明:如图2,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,

∴∠AEC=∠BFD,
在△CEH与△BFD中,
|
∴△CEH≌△BFD(ASA).
∴EH=FD,
在△ACH与△CBD中,
|
∴△ACH≌△CBD,
∴AH=CD,
∵AE=AH+EH,
∴AE=CD+DF.
看了 在Rt△ABC中,∠ACB=...的网友还看了以下:
如图,P是反比例函数y=kx(k>0)的图象上的任意一点,过P作x轴的垂线,垂足为M,已知△POM 2020-04-08 …
已知椭圆x2/4+y2/2=1(四分之x方+二分之y方=1),点A、B分别是它的左右定点,一条垂直 2020-04-27 …
如图,抛物线y=-5/4x^2+17/4x+1与y轴交于A点,过点A的直线与抛物线交于另一点B,过 2020-05-13 …
直线y=1/2x与双曲线y=k/x(k≠0)在第一象限交于A点,过点A作x轴的垂线,垂足为点M,已 2020-05-14 …
如图铁路上A;B两点相距二十五千米,C.D为村庄,A.D垂直于AB于A.BC垂直于AB于B.已知A 2020-06-28 …
抛物线y=-5/6x的平方7/6x+2,与x轴负半轴交于A点,与y轴交于B点,点H在第四象限的抛物 2020-07-26 …
如图所示,点电荷A、B所带电荷量分别为+2Q、-Q,a、b是A、B连线的中垂线上的两点,下列说法正 2020-08-01 …
数学二面角问题如果两个相交平面A,B,交线为CD,一条直线属于A,且垂直于CD,垂足为E,另一条直 2020-08-01 …
铁路上ab两点相距二十五千米,cd为两村庄,da垂直ab于a,cb垂直ab于b,已知da等于15千米 2020-11-20 …
根据题意自己画图.某社区要在AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA 2020-12-12 …