早教吧作业答案频道 -->数学-->
在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边△OBC,E是OC上的一点.(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;(2)如图2,点F是BC上的一点,将四
题目详情
在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边△OBC,E是OC上的一点.
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;
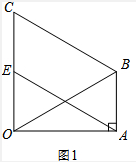
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.
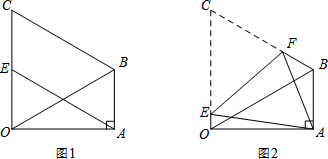
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.

▼优质解答
答案和解析
(1)证明:如图1,∵△OBC为等边三角形,
 ∴OC=OB,∠COB=60°.,
∴OC=OB,∠COB=60°.,
∵点E是OC的中点,
∴EC=
OC=
OB,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=
OB,∠COA=90°,
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2) 如图2,∵四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,
∴EC=EA,
∵OB=4,
∴OC=BC=4,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴OA=2
,
在Rt△OAE中,由(1)知:∠EOA=90°,
设OE=x,
∵OE2+OA2=AE2,
∴x2+(2
)2=(4-x)2,
解得,x=
,
∴OE=
.
 ∴OC=OB,∠COB=60°.,
∴OC=OB,∠COB=60°.,∵点E是OC的中点,
∴EC=
| 1 |
| 2 |
| 1 |
| 2 |
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=
| 1 |
| 2 |
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2) 如图2,∵四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,

∴EC=EA,
∵OB=4,
∴OC=BC=4,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴OA=2
| 3 |
在Rt△OAE中,由(1)知:∠EOA=90°,
设OE=x,
∵OE2+OA2=AE2,
∴x2+(2
| 3 |
解得,x=
| 1 |
| 2 |
∴OE=
| 1 |
| 2 |
看了 在△OAB中,∠OAB=90...的网友还看了以下:
如图,反比例函数y=k/x的图像经过点A(-根号3,b),过点A作AB⊥x轴于点B,△OAB的面积 2020-04-05 …
已知反比例函数y=k/x的图像经过A(-根号3,b),过点A作AB⊥x轴,交x轴于点B,△AOB的 2020-04-05 …
如图,已知反比例函数y=k/x的图像经过点A(-3/2,b),过点A作AB⊥x轴于点B,△AOB的 2020-04-08 …
如图竖立在点B处的标杆AB=2.5米,某观察者站立在点F处,从点E处看到杆顶A,树顶C在一直线上( 2020-05-17 …
如图,已知点A(2,0),点B在y轴正半轴上,且OB=1/2OA,将点B绕点A顺时针方向旋转90度 2020-06-13 …
如图已知抛物线Y=1/2X+bx+C经过点A(4,0)和点(0,4),交X轴于点C,过OB的中点, 2020-06-14 …
(2013•大连一模)如图所示,甲、乙两个小球从同一同定斜面的顶端0点水平抛出,分别落到斜面上的A 2020-06-16 …
四、阅读语段,答题。一个人握住一个鸡蛋使劲地捏,无论怎样用力也不能把它捏碎。薄薄(báobó)的鸡 2020-07-12 …
四、阅读语段,答题。一个人握住一个鸡蛋使劲地捏,无论怎样用力也不能把它捏碎。薄薄(báobó)的鸡 2020-07-12 …
直线l过原点和点(3,5),位于第一象限的点A在直线l上,x轴上有一点B,它的坐标为16,0角AB 2020-07-22 …