早教吧作业答案频道 -->数学-->
(本小题满分12分)已知二次曲线Ck的方程:.(Ⅰ)分别求出方程表示椭圆和双曲线的条件;(Ⅱ)若双曲线Ck与直线y=x+1有公共点且实轴最长,求双曲线方程
题目详情
(本小题满分12分)已知二次曲线Ck的方程: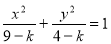 .
.
(Ⅰ)分别求出方程表示椭圆和双曲线的条件;
(Ⅱ)若双曲线Ck与直线y=x+1有公共点且实轴最长,求双曲线方程
▼优质解答
答案和解析
(Ⅰ)即k<4时,方程表示椭圆. 当即4<k<9时,方程表示双曲线(Ⅱ)
分 析:
(1)椭圆双曲线标准方程的特点(2)解决直线和椭圆的问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式.第四步:根据题设条件求解问题中结论.试题
解析:
(Ⅰ)当且仅当,即k<4时,方程表示椭圆.当且仅当(9-k)(4-k)<0,即4<k<9时,方程表示双曲线.(Ⅱ)解法一:由化简得,(13-2k)x2+2(9-k)x+(9-k)(k-3)=0∵Δ≥0,∴k≥6或k≤4(舍)∵双曲线实轴最长,∴k取最小值6时,9-k最大即双曲线实轴最长,此时双曲线方程为.解法二:若Ck表示双曲线,则k∈(4 9),不妨设双曲线方程为,联立消去y得,(5-2a2)x2-2a2x-6a2+a4=0∵Ck与直线y=x+1有公共点,∴Δ=4a4-4(5-2a2)(a4-6a2)≥0,即a4-8a2+15≥0,∴a2≤3或a2≥5(舍),∵双曲线实轴最长,应取3,此时双曲线方程为
考点:
椭圆双曲线标准方程的特点,求双曲线方程
分 析:
(1)椭圆双曲线标准方程的特点(2)解决直线和椭圆的问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式.第四步:根据题设条件求解问题中结论.试题
解析:
(Ⅰ)当且仅当,即k<4时,方程表示椭圆.当且仅当(9-k)(4-k)<0,即4<k<9时,方程表示双曲线.(Ⅱ)解法一:由化简得,(13-2k)x2+2(9-k)x+(9-k)(k-3)=0∵Δ≥0,∴k≥6或k≤4(舍)∵双曲线实轴最长,∴k取最小值6时,9-k最大即双曲线实轴最长,此时双曲线方程为.解法二:若Ck表示双曲线,则k∈(4 9),不妨设双曲线方程为,联立消去y得,(5-2a2)x2-2a2x-6a2+a4=0∵Ck与直线y=x+1有公共点,∴Δ=4a4-4(5-2a2)(a4-6a2)≥0,即a4-8a2+15≥0,∴a2≤3或a2≥5(舍),∵双曲线实轴最长,应取3,此时双曲线方程为
考点:
椭圆双曲线标准方程的特点,求双曲线方程
看了 (本小题满分12分)已知二次...的网友还看了以下:
用max{a,b,c}表示a,b,c中的最大者,若x,y,z均为正数,则{x^2+y^2,xy+z 2020-04-27 …
在△ABC中,内角A,B,C对边的边长分别是a,b,c已知c=2,c=π/3若sin(A+C)=2 2020-06-27 …
在△ABC中,角A,B,C对的边分别为a,b,c,且c=2,C=60°,若a+b=ab,求△ABC 2020-07-09 …
在△ABC中,∠A,∠B,∠C对边a、b、c,已知c=2,∠C=π/3.①若S△ABC=根号3,求 2020-07-22 …
若2*8的N次方*16的N次方=2的22次方求N的值.若2的a次方=32的B次方=52的C次方=3 2020-07-22 …
在三角形中ABC,角A、B、C对边分别为a、b、c.已知c=2.C=60°.若sinC+sin(B 2020-07-30 …
1.(a+b-c)的2次幂(c-a-b)的3次幂+(c-a-b)(a+b-c)的4次幂2.若2的a 2020-08-01 …
已知二次函数y=ax平方+bx+c,(1)若a=2,b+c=-2,b>c,且二次函数的图像经过点(p 2020-12-08 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …
在△ABC中,内角ABC对边的边长分别是abc,已知c=2,C=π/3,若sinC+sin(B-A) 2021-02-07 …