早教吧作业答案频道 -->数学-->
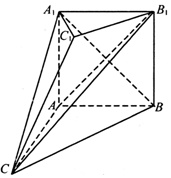
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且B1C1=12BC.(I)求证:A1B⊥B1C;(II)求证:AB1∥平面A1C1C.
题目详情
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且B1C1=
BC.
(I)求证:A1B⊥B1C;
(II)求证:AB1∥平面A1C1C.
| 1 |
| 2 |
(I)求证:A1B⊥B1C;
(II)求证:AB1∥平面A1C1C.

▼优质解答
答案和解析
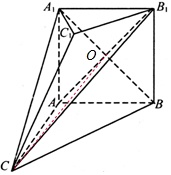 (I)证明:设A1B与AB1交于点O,连接CO.
(I)证明:设A1B与AB1交于点O,连接CO.
四边形ABB1A1是正方形,
∴A1B⊥AB1,A1O=BO,
∴在△A1BC中,A1C=BC,∴A1B⊥CO.
又因为A1B∩CO=O,∴A1B⊥面AB1C,
又B1C⊂面AB1C,A1B⊥B1C;
(Ⅱ)取BC中点D,连接AD,C1D,BB1D.
∵
∴四边形B1C1CD是平行四边形.
∴B1D∥CC1,B1B∥C1D,又B1B∥A1A,B1B=A1A,∴A1A∥C1D,A1A=C1D,
∴四边形A1ADC1是平行四边形.∴AD∥A1C1.
又B1D⊄面A1C1C,AD⊄面A1C1C,∴B1D∥面A1C1C,AD∥面A1C1C,
又B1D∩AD=D,∴平面.AB1D∥面A1C1C,
∵AB1⊂面AB1D,∴AB1∥平面A1C1C.
 (I)证明:设A1B与AB1交于点O,连接CO.
(I)证明:设A1B与AB1交于点O,连接CO.四边形ABB1A1是正方形,
∴A1B⊥AB1,A1O=BO,
∴在△A1BC中,A1C=BC,∴A1B⊥CO.
又因为A1B∩CO=O,∴A1B⊥面AB1C,
又B1C⊂面AB1C,A1B⊥B1C;
(Ⅱ)取BC中点D,连接AD,C1D,BB1D.
∵
|
∴B1D∥CC1,B1B∥C1D,又B1B∥A1A,B1B=A1A,∴A1A∥C1D,A1A=C1D,
∴四边形A1ADC1是平行四边形.∴AD∥A1C1.
又B1D⊄面A1C1C,AD⊄面A1C1C,∴B1D∥面A1C1C,AD∥面A1C1C,
又B1D∩AD=D,∴平面.AB1D∥面A1C1C,
∵AB1⊂面AB1D,∴AB1∥平面A1C1C.
看了 如图,在多面体ABC-A1B...的网友还看了以下:
坐标平面内有4个点A(0,2)B(-1,0)C(1,-1)D(3,0).(1)建立坐标系,描出四个 2020-05-21 …
一、我们知道1/1×2=1/1-1/2=1/2,1/2×3=1/2-1/3=1/6验证:1/3×4 2020-07-17 …
关于x的方程x+1/x=c+1/c的解是x1=c,x2=1/c;x-1/x=c-c/1(即x+(- 2020-07-21 …
直角三角形1:1:根号2请问各路高手:直角三角形三个角分别为30°60°90°我想问的是:1:1: 2020-07-22 …
学期期末复习中,我们已遇到了这样的问题:“已知ab/a+b=1/2,bc/b+c=1/3,ca/c 2020-07-22 …
以知△ABC的三边长分别为abc,且满足abc=2(a-1)(b-1)(c-1)1.是否存在边长为 2020-07-22 …
寻找规律解数学题1/1*2=1-1/22/2*3=1/2-1/31/3*4=1/3-1/4……计算 2020-07-22 …
数列{an}的前n项和为sn,且sn=(c+1)-can,(c不等于0,c不等于-1)数列{an} 2020-07-23 …
已知直角坐标系平面内点A(4,0)B(2,-2),C(1,1)在直角坐标平面内求一点P,使点A,B 2020-07-31 …
由下列各式:1>1/2,1+1/2+1/3>1有下列各式:1>1/2;1+1/2+1/3>1;1+1 2020-10-30 …