早教吧作业答案频道 -->数学-->
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.(1)求此抛物线的解析式;(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用
题目详情
如图,已知抛物线经过点A(-1,0),B(3,0),C(0,3)三点.
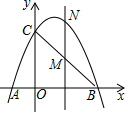
(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,请说明理由.

(1)求此抛物线的解析式;
(2)若点M是线段BC上的点(不与B,C重合),过M作NM∥y轴交抛物线于N,设点M的横坐标为m,请用含m的代数式表示MN的长;
(3)在(2)的条件下,连接NB,NC,是否存在点M,使△BNC的面积最大?若存在,求m的值;若不存在,请说明理由.
▼优质解答
答案和解析
(1)设抛物线的解析式为:y=a(x+1)(x-3),则:
a(0+1)(0-3)=3,a=-1;
∴抛物线的解析式:y=-(x+1)(x-3)=-x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
,
解得
;
故直线BC的解析式:y=-x+3.
 已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);
已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);
∴故MN=-m2+2m+3-(-m+3)=-m2+3m(0<m<3).
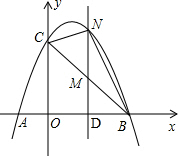
(3)如图;
∵S△BNC=S△MNC+S△MNB=
MN(OD+DB)=
MN•OB,
∴S△BNC=
(-m2+3m)•3=-
(m-
)2+
(0<m<3);
∴当m=
时,△BNC的面积最大,最大值为
.
a(0+1)(0-3)=3,a=-1;
∴抛物线的解析式:y=-(x+1)(x-3)=-x2+2x+3.
(2)设直线BC的解析式为:y=kx+b,则有:
|
解得
|
故直线BC的解析式:y=-x+3.
 已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);
已知点M的横坐标为m,MN∥y,则M(m,-m+3)、N(m,-m2+2m+3);∴故MN=-m2+2m+3-(-m+3)=-m2+3m(0<m<3).
(3)如图;
∵S△BNC=S△MNC+S△MNB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BNC=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 8 |
∴当m=
| 3 |
| 2 |
| 27 |
| 8 |
看了 如图,已知抛物线经过点A(-...的网友还看了以下:
如图所示,正比例函数y=ax的图像与反比例函数y=k/x的图像交于点A(3,2)M(m,n)是反比 2020-04-08 …
已知M是反比例函数y=x分之k(k≠0)图象上一点.过点M分别向x轴和y轴引垂线,如果它们与已知M 2020-04-08 …
焦点在坐标轴上,过点m(3,4)且虚轴长是实轴长的2倍,求双曲线标准方程 2020-05-13 …
如图,二次函数y=ax^2+bx+c的图像交x轴于A(-2,0)B(1,0)交y轴于点C(0,-2 2020-05-16 …
已知椭球面x∧2+2Y∧2+z∧2=4上过点M的切面平行于平面4x-8y+4z-5=0求M的坐标. 2020-06-14 …
已知,M是等边△ABC边BC上的点.(1)如图1,过点M作MN∥AC且交于点N,求证:BM=BN; 2020-06-18 …
(2014•淮安)如图,点A(1,6)和点M(m,n)都在反比例函数y=kx(x>0)的图象上,( 2020-07-22 …
如图,动点M在以O为圆心,AB为直径的半圆弧上运动(点M不与点A、B及AB的中点F重合),连接OM 2020-07-24 …
中点在原点,焦点在坐标轴上,过点M(3,4),且虚轴长是实轴长的2倍的双曲线方程为 2020-07-30 …
如图,质量为M的木块中间有一个竖直的槽,槽内夹着一个质量为m的木块,用一个竖直向上的力F拉m,使m在 2020-11-08 …