早教吧作业答案频道 -->数学-->
如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB(1)求两个函数的解析式;(2)直线AB交x轴于点C,求△AOC的面积;(3)在x轴上存在一点p,使△AOP是等腰三
题目详情
如图,已知一个正比例函数与一个一次函数的图象交于点A(3,4),且OA=OB
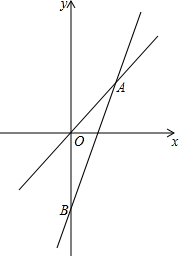
(1)求两个函数的解析式;
(2)直线AB交x轴于点C,求△AOC的面积;
(3)在x轴上存在一点p,使△AOP是等腰三角形,直接写出所有符合要求的点P的坐标.

(1)求两个函数的解析式;
(2)直线AB交x轴于点C,求△AOC的面积;
(3)在x轴上存在一点p,使△AOP是等腰三角形,直接写出所有符合要求的点P的坐标.
▼优质解答
答案和解析
(1)设直线OA为y=kx.
∵y=kx经过点(3,4),
∴3k=4,k=
,
∴y=
x.
设直线AB为y=ax+b,
∵y=ax+b经过(3,4),(0,-5),
∴
,
解得:
,
∴y=3x-5.
(2)S△AOB=
|OB|×3=
×5×3=7.5;
(3)把(3,4)代入y1=k1x得到:3k1=4,
解得:k1=
,
当OA是底边时,OA的中点是(
,2),设过OA的中点且与OA垂直的直线的解析式是:y=-
x+b,
根据题意得:b=
,
直线的解析式是:y=-
x+
,
当y=0时,x=
,
则P的坐标是(
,0);
当OA是腰,O是顶角的顶点时,OP=OA=5,则P的坐标是(5,0)或(-5,0);
当OA是腰,A是顶角的顶点时,AP=AO,则P与O关于x=3对称,则P的坐标是(6,0).
则P的坐标是:(
,0)或(5,0)或(-5,0)或(6,0).
∵y=kx经过点(3,4),
∴3k=4,k=
| 4 |
| 3 |
∴y=
| 4 |
| 3 |
设直线AB为y=ax+b,
∵y=ax+b经过(3,4),(0,-5),
∴
|
解得:
|
∴y=3x-5.
(2)S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)把(3,4)代入y1=k1x得到:3k1=4,
解得:k1=
| 4 |
| 3 |
当OA是底边时,OA的中点是(
| 3 |
| 2 |
| 3 |
| 4 |
根据题意得:b=
| 25 |
| 8 |
直线的解析式是:y=-
| 3 |
| 4 |
| 25 |
| 8 |
当y=0时,x=
| 25 |
| 6 |
则P的坐标是(
| 25 |
| 6 |
当OA是腰,O是顶角的顶点时,OP=OA=5,则P的坐标是(5,0)或(-5,0);
当OA是腰,A是顶角的顶点时,AP=AO,则P与O关于x=3对称,则P的坐标是(6,0).
则P的坐标是:(
| 25 |
| 6 |
看了 如图,已知一个正比例函数与一...的网友还看了以下:
初三几何几何达人进!题目是这样的:如图,直线l经过⊙O,且交于A、B两点,点C在⊙O上,且∠AOC= 2020-03-31 …
数学比例尺问题1.已知线段a,b,c,d是成比例线段,且a=2cm,b=0.6cm,c=4cm,那 2020-04-13 …
九上数学题圆如图三角形ABC内接于圆o且BC是圆0的直径如图,三角形ABC内接于圆o,且BC是圆o 2020-06-03 …
如图,某铁路MN与公路PQ相交于点O,且角NOQ=60度,某仓库G在A区,到公路和铁路距离相等,且 2020-06-06 …
设A为实方针,证明(1)如果A=At(转置矩阵),且A^2=O,则A=O;(2)如果A*AT=O, 2020-06-22 …
求几个有歧义的句子,要搞笑的!必须是歧义,而且搞笑我先举个例子:一个SOSO用户在SOSO中提了一 2020-07-03 …
关于圆的内接三角形简单问题一个圆O,其中有一个等腰三角形ABC,等腰三角形ABC内接于圆O,且两腰 2020-07-04 …
已知抛物线y=(x-b)2+m-b的顶点为m与轴交于点A(x1,O),B(x2,O),且△MAB为 2020-07-12 …
如图CM、CN分别△ABC的内角、外角平分线,O是AC上的点,直线L经过点O且L‖BC交CM如图C 2020-07-20 …
如图a直线l经过圆o的圆心o,且与圆o交于A,B两点,点c在圆o上且点C在圆o上,且∠AOC=30 2020-07-26 …