早教吧作业答案频道 -->数学-->
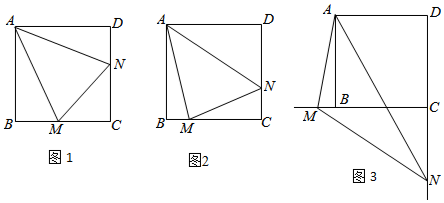
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.(1)当∠MAN绕点A旋转到BM=DN时(如图1),易证MN=BM+DN.(2)当∠MAN绕点A旋转到BM
题目详情
已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M,N.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),易证MN=BM+DN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?写出猜想,并加以证明.
(1)当∠MAN绕点A旋转到BM=DN时(如图1),易证MN=BM+DN.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),线段BM,DN和MN之间有怎样的数量关系?写出猜想,并加以证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM,DN和MN之间又有怎样的数量关系?写出猜想,并加以证明.

▼优质解答
答案和解析
(1)如图1,连接AC,交MN于点G,
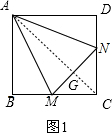
∵四边形ABCD为正方形,
∴BC=CD,且BM=DN,
∴CM=CN,且AC平分∠BCD,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG,
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,
∴∠BAM=∠GAN=∠GAM,
在△ABM和△AGM中,
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN,
∴BM+DN=MN;
(2)猜想:BM+DN=MN,
证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE,
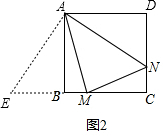
在△ABE和△ADN中,
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,
∴∠EAM=∠NAM,
在△AEM和△ANM中
∴△AEM≌△ANM(SAS),
∴ME=MN,
又ME=BE+BM=BM+DN,
∴BM+DN=MN;
(3)DN-BM=MN.
证明如下:
如图3,在DC上截取DF=BM,连接AF,
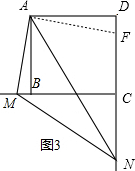
△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN-DF=DN-BM,
∴DN-BM=MN.

∵四边形ABCD为正方形,
∴BC=CD,且BM=DN,
∴CM=CN,且AC平分∠BCD,
∴AC⊥MN,且MG=GN,
∴∠MAG=∠NAG,
∵∠BAC=∠MAN=45°,即∠BAM+∠GAM=∠GAM+∠GAN,
∴∠BAM=∠GAN=∠GAM,
在△ABM和△AGM中,
|
∴△ABM≌△AGM(AAS),
∴BM=MG,同理可得GN=DN,
∴BM+DN=MG+GN=MN,
∴BM+DN=MN;
(2)猜想:BM+DN=MN,
证明如下:
如图2,在MB的延长线上,截取BE=DN,连接AE,

在△ABE和△ADN中,
|
∴△ABE≌△ADN(SAS),
∴AE=AN,∠EAB=∠NAD,
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠EAB+∠BAM=45°,
∴∠EAM=∠NAM,
在△AEM和△ANM中
|
∴△AEM≌△ANM(SAS),
∴ME=MN,
又ME=BE+BM=BM+DN,
∴BM+DN=MN;
(3)DN-BM=MN.
证明如下:
如图3,在DC上截取DF=BM,连接AF,

△ABM和△ADF中,
|
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∴∠BAM+∠BAF=∠BAF+∠DAF=90°,即MAF=∠BAD=90°,
∵∠MAN=45°,
∴∠MAN=∠FAN=45°,
在△MAN和△FAN中,
|
∴△MAN≌△FAN(SAS),
∴MN=NF,
∴MN=DN-DF=DN-BM,
∴DN-BM=MN.
看了 已知:正方形ABCD中,∠M...的网友还看了以下:
这题m点不知道,sd垂直abcd且abcd为矩形 角abm 60度 我就是看不懂那个m点怎么设出来 2020-05-16 …
已知P是抛物线y^2=2x上的动点,点P到准线的距离为d,且点P在y轴上的射影是M,点A(3.5, 2020-05-22 …
诺f(x)是在[a,b]上的正值可微函数,则有点m属于(a,b),使:In[f(b)/f(a)]= 2020-06-13 …
A,B是直线L外同侧的两点,且点A知点B到L的距离分别是3厘米和5厘米,AB=2√2厘米,若点P在 2020-06-20 …
已知椭圆x2/25+y2/9=1上一点为M,点A(2,2)是椭圆内一点,F1、F2为它的左右焦点, 2020-06-21 …
已知椭圆x2/25+y2/9=1上一点为M,点A(2,2)是椭圆内一点,F1、F2为它的左右焦点, 2020-06-21 …
当m,n是正实数,且满足m+n=mn时,就称点P(m,mn)为“完美点”,已知点A(0,5)与点M 2020-07-29 …
(1)点(-1,-1)在直线l上的射影为双曲线x^2-y^2=1的左焦点,则l的方程是(2)已知点 2020-07-30 …
已知点P为抛物线y^2=2x上的动点,点P在y轴上的射影是M,点A的坐标是A(7/2,4),则|P 2020-07-30 …
已知P是抛物线y∧2=2x上的一个动点,点P到准线的距离为d,且点p到y轴上的射影为M,点A(7| 2020-07-31 …