早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0
题目详情
如图,在平面直角坐标系中,有一组有规律的点:A1(0,1)、A2(1,0)、A3(2,1)、A4(3,0)、A5(4,1),…依此规律可知,当n为奇数时,有点An(n-1,1);当n为偶数时,有点An(n-1,0).抛物线C1经过A1、A2、A3三点,抛物线C2经过A2、A3、A4三点,抛物线C3经过抛物线A3、A4、A5三点,…,抛物线Cn经过An、An+1、An+2.
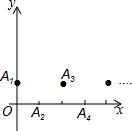
(1)找规律:C1的对称轴为x=___,C2的对称轴为x=___;并直接写出抛物线C3、C4的解析式.
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=30时,求线段EF的长.
(3)若直线x=m分别交x轴、抛物线C999、抛物线C1000于点P、M、N,作直线A1000M、A1000N,当∠PA1000M=45°时,求sin∠PA1000M的值.

(1)找规律:C1的对称轴为x=___,C2的对称轴为x=___;并直接写出抛物线C3、C4的解析式.
(2)若点E(e,f1)、F(e,f2)分别在抛物线C27、C28上,当e=30时,求线段EF的长.
(3)若直线x=m分别交x轴、抛物线C999、抛物线C1000于点P、M、N,作直线A1000M、A1000N,当∠PA1000M=45°时,求sin∠PA1000M的值.
▼优质解答
答案和解析
(1)∵A1(0,1)、A2(1,0)、A3(2,1)
∴A1(0,1)、A3(2,1)关于x=1对称,
∴C1的对称轴为x=1,
同理C2的对称轴为x=2,
故答案为1,2;
由顶点式求出C3的解析式为:y=(x-3)2,C4的解析式为:y=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
∴当e=30时,f1=(30-27)2=9,f2=(30-28)2+1=5,
∴EF=f1-f2=4.
(3)由(2)中发现的规律可知,抛物线C999、C1000解析式分别为:y=(x-999)2,
y=-(x-1000)2+1.
点A1000坐标为(999,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图
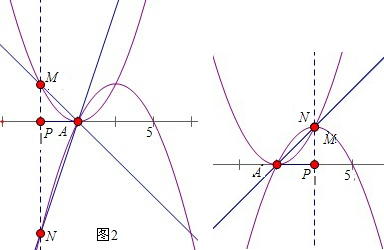
在A1000(999,0)点左侧,当m=998时,M(998,1)此时有∠PA1000M=45°,N(998,-3),相应的sin∠PA1000N的值为
;
在A1000(999,0)点右侧,当m=1000时,M(1000,1)此时有∠PA1000M=45°,N(1000,1),相应的sin∠PA1000N的值为
.
∴A1(0,1)、A3(2,1)关于x=1对称,
∴C1的对称轴为x=1,
同理C2的对称轴为x=2,
故答案为1,2;
由顶点式求出C3的解析式为:y=(x-3)2,C4的解析式为:y=-(x-4)2+1.
(2)由特殊出发,可以发现这组抛物线解析式的特点:
y1=(x-1)2,
y2=-(x-2)2+1,
y3=(x-3)2,
y4=-(x-4)2+1,
…
∴抛物线C27、C28的解析式应该为:y27=(x-27)2,y28=-(x-28)2+1.
∴当e=30时,f1=(30-27)2=9,f2=(30-28)2+1=5,
∴EF=f1-f2=4.
(3)由(2)中发现的规律可知,抛物线C999、C1000解析式分别为:y=(x-999)2,
y=-(x-1000)2+1.
点A1000坐标为(999,0).
顺便指向,由(2)的研究经验发现,可以退回简单的抛物线C3、C4的情况来研究.分以下两种情况,如图

在A1000(999,0)点左侧,当m=998时,M(998,1)此时有∠PA1000M=45°,N(998,-3),相应的sin∠PA1000N的值为
3
| ||
| 10 |
在A1000(999,0)点右侧,当m=1000时,M(1000,1)此时有∠PA1000M=45°,N(1000,1),相应的sin∠PA1000N的值为
| ||
| 2 |
看了 如图,在平面直角坐标系中,有...的网友还看了以下:
数学分析题一道,一百分奖赏一道数学题,数学分析题file:///d:/我的文档/桌面/201012 2020-06-03 …
求解一道高数证明题设f(x)在(0,1)上连续,在(0,1)内二阶可导,且f(0)=f(1)=0, 2020-06-13 …
1.设f(x)在[0,1]上连续,且f(0)=f(1),证明:存在x0∈[0,1],使得f(x0) 2020-06-18 …
f(x)在[0,1]连续,在(0,1)可导.f(0)=0,f(1)=1.证明存在两点a,b属于(f 2020-06-18 …
在0.1•4、0.•1•4、0.1414、0.144四个数中,最大的数是0.1•40.1•4,最小 2020-06-27 …
设函数f(x)在〔0,1〕上连续,在(0,1)内可导,且f(0)=f(1)=0,证明在(0,1)内 2020-07-16 …
已知函数f(x)=9^x-3^(x+1)+c(其中是常数)若当x∈0,1时,恒有f(x)<0,求实 2020-07-21 …
若f(x)在0,1上连续,在(0,1)内可导,且f(0)=f(1)=0,f(1/2)=1,证明:在 2020-07-22 …
F(x)在[0,1]上二阶可导,且limx->0f(x)/x=1,limx->1f(x)/x-1= 2020-07-26 …
不定积分题和其他题.F(x)在[0,1]上二阶可导,且limx->0f(x)/x=1,limx-> 2020-07-30 …