早教吧作业答案频道 -->数学-->
如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为何()A、45B、52.5C、67.5D、75
题目详情
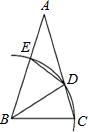 如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为何( )
如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC、AB于D,E两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE的度数为何( )| A、45 | B、52.5 | C、67.5 | D、75 |
▼优质解答
答案和解析
分析:
根据AB=AC,利用三角形内角和定理求出∠ABC的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠BDE的度数.
∵AB=AC,∴∠ABC=∠ACB,∵∠A=30°,∴∠ABC=∠ACB=12(180°-30°)=75°,∵以B为圆心,BC长为半径画弧,∴BE=BD=BC,∴∠BDC=∠ACB=75°,∴∠CBD=180°-75°-75°=30°,∴∠DBE=75°-30°=45°,∴∠BED=∠BDE=12(180°-45°)=67.5°.故选C.
点评:
本题考查了学生对等腰三角形的性质和三角形内角和定理等知识点的理解和掌握,此题的突破点是利用等腰三角形的性质和三角形内角和定理求出∠DBC=45°,然后即可求得答案.
分析:
根据AB=AC,利用三角形内角和定理求出∠ABC的度数,再利用等腰三角形的性质和三角形内角和定理求出∠DBC=30°,然后即可求出∠BDE的度数.
∵AB=AC,∴∠ABC=∠ACB,∵∠A=30°,∴∠ABC=∠ACB=12(180°-30°)=75°,∵以B为圆心,BC长为半径画弧,∴BE=BD=BC,∴∠BDC=∠ACB=75°,∴∠CBD=180°-75°-75°=30°,∴∠DBE=75°-30°=45°,∴∠BED=∠BDE=12(180°-45°)=67.5°.故选C.
点评:
本题考查了学生对等腰三角形的性质和三角形内角和定理等知识点的理解和掌握,此题的突破点是利用等腰三角形的性质和三角形内角和定理求出∠DBC=45°,然后即可求得答案.
看了 如图,△ABC中,以B为圆心...的网友还看了以下:
已知F1,F2分别是双曲线C:x2a2-y2b2=1(a>0,b>0)的左,右焦点,G是双曲线C上 2020-05-15 …
已知一个圆的圆心为M(2,-3),一条直径的两个端点分别在X轴上和Y轴上,则此圆的方程式是 ( ) 2020-05-16 …
从一副扑克牌中(52张)中一张接一张有放回的抽取4次,所抽的4张牌的花色各不相同的概率分母:52的 2020-06-13 …
如图,△AOB中,∠B=30°.将△AOB绕点O顺时针旋转52°得到△A′OB′,边A′B′与边O 2020-06-20 …
(2013•河南模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC, 2020-07-09 …
(2014•烟台)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点 2020-07-17 …
已知H2S的一级和二级电离平衡常数分别为Ka(H2S)=9.1×10-8,Ka(HS-)=1.1× 2020-07-17 …
设直线l:3x+4y+a=0,圆C:(x-2)2+y2=2,若在圆C上存在两点P,Q,在直线l上存 2020-07-21 …
已知Rt△ABC的斜边AB的长为4,设P是以C为圆心1为半径的圆上的任意一点,则PA•PB的取值范 2020-07-30 …
某校男女生人数分别为312人、288人,则男生人数占全校总人数的百分比为()A.48%B.52%C. 2020-11-20 …