早教吧作业答案频道 -->数学-->
在△ABC中,H为垂心,G为重心,O为外心,求证:.
题目详情
在△ABC中,H为垂心,G为重心,O为外心,求证: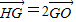 .
.
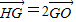 .
.▼优质解答
答案和解析
分析:
分析:
根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得 =+,由向量相等和向量的减法运算进行转化,得到 ,再根据△ABC重心为G满足 =,结合已知中 ,我们易判断出 =3 ,根据数乘向量的几何意义,即可得到O,G,H三点共线,且OG:GH=1:2即可.
如图:作直径BD,连接DA、DC,由图得,=-,∵H为△ABC的垂心,∴CH⊥AB,AH⊥BC,∵BD为直径,∴DA⊥AB,DC⊥BC∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,∴=又∵=-=+,∴=+=+=++,∵G为△ABC的重心∴=3 =3 +=即 =3 即O,G,H三点共线,且OH=3OG即O,G,H三点共线,且OG:GH=1:2.从而得到:.
点评:
点评:
本题考查的知识点是三角形的五心,其中熟练掌握向量五心的向量表达式形式,如(1)中△ABC外心为O满足 ,(2)中△ABC重心为G满足 =,是解答此类问题的关键.
分析:
分析:
根据题意作出图形,由外心和垂心的性质证明四边形AHCD是平行四边形,由向量加法的三角形法则得 =+,由向量相等和向量的减法运算进行转化,得到 ,再根据△ABC重心为G满足 =,结合已知中 ,我们易判断出 =3 ,根据数乘向量的几何意义,即可得到O,G,H三点共线,且OG:GH=1:2即可.
如图:作直径BD,连接DA、DC,由图得,=-,∵H为△ABC的垂心,∴CH⊥AB,AH⊥BC,∵BD为直径,∴DA⊥AB,DC⊥BC∴CH∥AD,AH∥CD,故四边形AHCD是平行四边形,∴=又∵=-=+,∴=+=+=++,∵G为△ABC的重心∴=3 =3 +=即 =3 即O,G,H三点共线,且OH=3OG即O,G,H三点共线,且OG:GH=1:2.从而得到:.
点评:
点评:
本题考查的知识点是三角形的五心,其中熟练掌握向量五心的向量表达式形式,如(1)中△ABC外心为O满足 ,(2)中△ABC重心为G满足 =,是解答此类问题的关键.
看了 在△ABC中,H为垂心,G为...的网友还看了以下:
AB为圆O直径,AD与圆O相切于A·(初3圆的几何)AB为圆O直径,AD与圆O相切于A,DE与圆O 2020-05-20 …
一杆秤如图,秤杆与秤钩的总重为G,重心在C点,O处为提纽,秤砣重为P,已知OA=a,OC=b.(1 2020-06-21 …
已知以点C(t,2/t)(t∈R,t≠0)为圆心的圆已经原点O,圆C分别交X轴,Y轴于点A,B,点 2020-07-26 …
设三角形ABC的外心为O,垂心为H,重心为G,求证:O,G,H三点共线且HG=2OG 2020-07-30 …
设△ABC的外心为O,重心为G,取点H,使OH=OA+OB+OC.求证:(Ⅰ)点H为△ABC的垂心 2020-07-30 …
设△ABC外心为O,重心为G.取点H,使OA+OB+OC=OH.求证:(1)H是△ABC的垂心;( 2020-07-30 …
用反证法证明:已知,在同一平面内有三条直线a,b,c,a⊥c,b⊥c.求证:a∥b.证明:假设所求 2020-08-01 …
怎么用余弦定理证明等腰(腰用a表示)三角形的底边(底边所对的角为o)=2asin(o/2)?为什么2 2020-10-31 …
探究:在图中找出一组相等的线段(半径除外),并证明你的结论.OA,OB是圆O的半径,且OA垂直OB, 2020-12-05 …
如图所示的杠杆(自重和摩擦不计),O为支点,A处挂一重为100N的物体,为保证杠杆在水平方向平衡,在 2020-12-05 …