早教吧作业答案频道 -->数学-->
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.(1)求证:△ADE≌△CBF;(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证
题目详情
已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
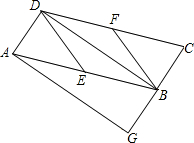
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.

(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=
AB,CF=
CD.
∴AE=CF.
在△AED和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2) 当四边形BEDF是菱形时,四边形AGBD是矩形.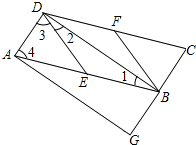
理由:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴▱四边形AGBD是矩形.
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CF.
在△AED和△CBF中,
|
∴△ADE≌△CBF(SAS).
(2) 当四边形BEDF是菱形时,四边形AGBD是矩形.

理由:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴▱四边形AGBD是矩形.
看了 已知:如图,在平行四边形AB...的网友还看了以下:
几ˋˊ何数学题自己先把图画出来吧图:一个由点A.B.C组成的等边三角形中,点D是边AB的中点,点E 2020-05-13 …
g形剖面图是根据等高线g形图绘制而成的.如图所示为我国南方某海岛的g形剖面图,据此完成4~5题.请 2020-05-16 …
设F是抛物线G:x2=4y的焦点.(Ⅰ)过点P(0,-4)作抛物线G的切线,求切线方程;(Ⅱ)过抛 2020-06-06 …
(1/2)已知函数f(x)=ax^2+1(a>0),g(x)=x^3+bx.若曲线f(x)与曲线g 2020-06-27 …
已知双曲线G的中心在原点,它的渐近线与圆相切,过点P(-4,0)作斜率为的直线l,使得l和G交于A 2020-08-01 …
一道解析几何体设F是抛物线Gy²=2px(p>0)的焦点,过F且与G的对称轴垂直的直线被抛物线G截 2020-08-02 …
下列反应符合下图p-v变化曲线的是()A.H2(g)+I2(g)2HI(g)B.3NO2(g)+H2 2020-10-30 …
3、某分部工程有A、B、C、D、E、F、G、H八道工序,其逻辑关系是:A完成后进行E、F.E完成后进 2020-12-01 …
如图1,直线L:y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线G:y=ax2+b 2020-12-26 …
已知抛物线G:y2=2px(p>0)与圆E:(x+p2)2+y2=r2(r>0),C,D抛物线上两点 2021-01-11 …