早教吧作业答案频道 -->数学-->
正四面体的棱长为46,顶点都在同一球面上,则该球的表面积为.
题目详情
正四面体的棱长为4
,顶点都在同一球面上,则该球的表面积为___.
| | 6 |
▼优质解答
答案和解析
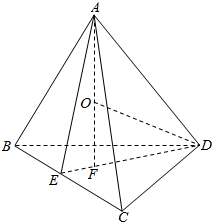 过D作DE⊥BC,交BC于E,过点A作AF⊥平面BCD,交DE于F,连结AE,
过D作DE⊥BC,交BC于E,过点A作AF⊥平面BCD,交DE于F,连结AE,
设O为正四面体A-BCD的外接球的球心,则O在AF上,连结OD,
∵正四面体A-BCD的棱长为4
,
∴E是BC中点,F是△BCD重心,
∴DF=
DE=
=4
,EF=
DE=2
,
AE=
=6
,AF=
=8,
设球O的半径OA=OC=R,
则R2=(8-R)2+(4
)2,
解得R=6,
∴该球的表面积S=4πR2=4π×36=144π.
故答案为:144π.
 过D作DE⊥BC,交BC于E,过点A作AF⊥平面BCD,交DE于F,连结AE,
过D作DE⊥BC,交BC于E,过点A作AF⊥平面BCD,交DE于F,连结AE,设O为正四面体A-BCD的外接球的球心,则O在AF上,连结OD,
∵正四面体A-BCD的棱长为4
| 6 |
∴E是BC中点,F是△BCD重心,
∴DF=
| 2 |
| 3 |
| 2 |
| 3 |
| 96-24 |
| 2 |
| 1 |
| 3 |
| 2 |
AE=
| 96-24 |
| 2 |
| 72-8 |
设球O的半径OA=OC=R,
则R2=(8-R)2+(4
| 2 |
解得R=6,
∴该球的表面积S=4πR2=4π×36=144π.
故答案为:144π.
看了 正四面体的棱长为46,顶点都...的网友还看了以下:
平行六面体与四面体的体积关系为什么平行六面体的体积是其中四面体体积的6倍?为什么呢? 2020-06-14 …
求不在同一平面四点体积的算法就是四面体的体积(x,y,z)、(x1,y1,z1)(x2,y2,z2 2020-06-14 …
任意多面体(包括凹多面体)体积怎么求?对于凸多面体,只需要在体内任取一点作为顶点,将多面体分割为多 2020-07-02 …
①棱长为1的正四面体与一个球①若正四面体的四个顶点都在球面上,则这个球的表面积3π23π2.②若球 2020-07-19 …
三角形的面积,a,b,c为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为 2020-07-23 …
空间中任意放置的棱长为2的正四面体.下列命题正确的是.(写出所有正确的命题的编号)①正四面体的主视 2020-07-31 …
四棱柱与其内接四面体的体积关系据说正方体的体积是其内接正四面体体积的3倍,请问一个任意的四棱柱的体 2020-07-31 …
空间中任意放置的棱长为2的正四面体.下列命题正确的是.(写出所有正确的命题的编号)①正四面体的主视 2020-08-01 …
(2010•宿州三模)下列命题:①四面体一定有外接球;②四面体一定有内切球;③四面体任三个面的面积之 2020-11-12 …
1.长方体的三个侧面面积为9,6,2,则它的体积是?2.将一个棱长为1的正方体木块锯成最大的一个正四 2020-12-24 …