早教吧作业答案频道 -->数学-->
已知椭圆C:,F1,F2分别为左,右焦点,离心率为,点A在椭圆C上,,,过F2与坐标轴不垂直的直线l交椭圆于P,Q两点.(1)求椭圆C的方程;(2)在线段OF2上是否存在点M(m
题目详情
已知椭圆C: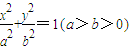 ,F 1 ,F 2 分别为左,右焦点,离心率为
,F 1 ,F 2 分别为左,右焦点,离心率为 ,点A在椭圆C上,
,点A在椭圆C上,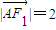 ,
,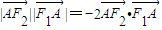 ,过F 2 与坐标轴不垂直的直线l交椭圆于P,Q两点.
,过F 2 与坐标轴不垂直的直线l交椭圆于P,Q两点.
(1)求椭圆C的方程;
(2)在线段OF 2 上是否存在点M(m,0),使得以线段MP,MQ为邻边的四边形是菱形?若存在,求出实数m的取值范围;若不存在,说明理由.
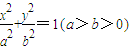 ,F 1 ,F 2 分别为左,右焦点,离心率为
,F 1 ,F 2 分别为左,右焦点,离心率为 ,点A在椭圆C上,
,点A在椭圆C上,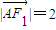 ,
,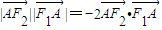 ,过F 2 与坐标轴不垂直的直线l交椭圆于P,Q两点.
,过F 2 与坐标轴不垂直的直线l交椭圆于P,Q两点.(1)求椭圆C的方程;
(2)在线段OF 2 上是否存在点M(m,0),使得以线段MP,MQ为邻边的四边形是菱形?若存在,求出实数m的取值范围;若不存在,说明理由.
▼优质解答
答案和解析
分析:
(1)在焦点三角形F1AF2中,由,可得顶角A的余弦值,由椭圆定义及离心率为,,即可将三边都用a表示,最后利用余弦定理列方程即可解得a值,进而得椭圆C的方程(2)先设出点P、Q的坐标及直线l的方程,代入椭圆方程,得关于x的一元二次方程,利用韦达定理得交点P、Q横坐标的和与积,再由存在点M(m,0),使得以线段MP,MQ为邻边的四边形是菱形,知,将坐标代入后可得m关于k的函数,求其值域,看是否符合题意即可
(1)由已知,∴2c=a,即|F1F2|=a∵,∴又∵,∴,在△F1AF2中,由余弦定理得,即a2-4a+4=0∴a=2∴c=1,b2=a2-c2=3,∴椭圆方程为.(2)假设存在点M(m,0)(0<m<1)满足条件,设P(x1,y1),Q(x2,y2),直线l的方程为y=k(x-1),联立:,∵直线l过焦点,∴△>0∴,∵线段MP,MQ为邻边的四边形是菱形∴∵,,,,∴,∵x2-x1≠0,k=∴x2+x1-2m+k(y2+y1)=0,∵y2+y1=k(x1-1)+k(x2-1)=k(x2+x1)-2k∴x2+x1-2m+k2(x2+x1-2)=0,∴,∴,∴,又∵M(m,0)在线段OF2上,则0<m<1,故存在满足题意.
点评:
本题考查了椭圆的标准方程及其几何性质,焦点三角形的性质,直线与椭圆的位置关系,特别是直线与椭圆相交时利用韦达定理,设而不求的技巧解决问题的能力
分析:
(1)在焦点三角形F1AF2中,由,可得顶角A的余弦值,由椭圆定义及离心率为,,即可将三边都用a表示,最后利用余弦定理列方程即可解得a值,进而得椭圆C的方程(2)先设出点P、Q的坐标及直线l的方程,代入椭圆方程,得关于x的一元二次方程,利用韦达定理得交点P、Q横坐标的和与积,再由存在点M(m,0),使得以线段MP,MQ为邻边的四边形是菱形,知,将坐标代入后可得m关于k的函数,求其值域,看是否符合题意即可
(1)由已知,∴2c=a,即|F1F2|=a∵,∴又∵,∴,在△F1AF2中,由余弦定理得,即a2-4a+4=0∴a=2∴c=1,b2=a2-c2=3,∴椭圆方程为.(2)假设存在点M(m,0)(0<m<1)满足条件,设P(x1,y1),Q(x2,y2),直线l的方程为y=k(x-1),联立:,∵直线l过焦点,∴△>0∴,∵线段MP,MQ为邻边的四边形是菱形∴∵,,,,∴,∵x2-x1≠0,k=∴x2+x1-2m+k(y2+y1)=0,∵y2+y1=k(x1-1)+k(x2-1)=k(x2+x1)-2k∴x2+x1-2m+k2(x2+x1-2)=0,∴,∴,∴,又∵M(m,0)在线段OF2上,则0<m<1,故存在满足题意.
点评:
本题考查了椭圆的标准方程及其几何性质,焦点三角形的性质,直线与椭圆的位置关系,特别是直线与椭圆相交时利用韦达定理,设而不求的技巧解决问题的能力
看了 已知椭圆C:,F1,F2分别...的网友还看了以下:
椭圆方程与圆的方程椭圆C:x²/a²+y²/b²=1(a>b>0)的离心率为3/5,两焦点分别是F 2020-05-15 …
椭圆C的焦点在x轴上焦距为2,直线l:x-y-1=0与椭圆C交于A、B两点,F1是左焦点F1A⊥F 2020-05-15 …
一、已知椭圆的焦点F1(0,-1)F2(0,1)离心率e=1/2 (1)求该椭圆方程(2)设点p在 2020-05-16 …
椭圆有两焦点坐标分别为F1负根号3,0),F2(根号3,0),且椭圆过点(1、负根号3/2),求求 2020-05-23 …
在直线x-y+9=0上任取一点P,过点P以椭圆x^/12+y^/3=1的焦点为焦点做椭圆1)P点在 2020-06-17 …
问一道解析几何关于椭圆的椭圆焦点在x轴椭圆上的点到焦点最远距离3最短距离1(1)求椭圆方程(2)若 2020-06-30 …
在一个椭圆中以焦点f1,f2为直径两端点的圆,恰好过椭圆短轴的两个端点,求椭圆离心率参考答案中说b 2020-07-21 …
悬挂在弹簧测力计下重为G的物块,分别在力F1、F2作用下的运动情况如图所示,则关于弹簧测力计的示数 2020-07-22 …
已知椭圆的焦点是F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C上且PF1的绝对 2020-07-26 …
椭圆X^2/4+Y^2+1,左焦点为F1,椭圆上有一点P,过P点切线为L2,设F1P延长线为L1,分 2020-11-01 …