早教吧作业答案频道 -->数学-->
对于函数f(x)(x∈D),若存在正常数T,使得对任意的x∈D,都有f(x+T)≥f(x)成立,我们称函数f(x)为“T同比不减函数”.(1)求证:对任意正常数T,f(x)=x2都不是“T同比不减函
题目详情
对于函数f(x)(x∈D),若存在正常数T,使得对任意的x∈D,都有f(x+T)≥f(x)成立,我们称函数f(x)为“T同比不减函数”.
(1)求证:对任意正常数T,f(x)=x2都不是“T同比不减函数”;
(2)若函数f(x)=kx+sinx是“
同比不减函数”,求k的取值范围;
(3)是否存在正常数T,使得函数f(x)=x+|x-1|-|x+1|为“T同比不减函数”;若存在,求T的取值范围;若不存在,请说明理由.
(1)求证:对任意正常数T,f(x)=x2都不是“T同比不减函数”;
(2)若函数f(x)=kx+sinx是“
| π |
| 2 |
(3)是否存在正常数T,使得函数f(x)=x+|x-1|-|x+1|为“T同比不减函数”;若存在,求T的取值范围;若不存在,请说明理由.
▼优质解答
答案和解析
 (1)∵f(x)=x2,
(1)∵f(x)=x2,
∴f(x+T)-f(x)=(x+T)2-x2=2xT+T2=T(2x+T),
由于2x+T与0的小无法比较,
∴f(x+T)≥f(x)不一定成立,
∴对任意正常数T,f(x)=x2都不是“T同比不减函数,
(2)∵函数f(x)=kx+sinx是“
同比不减函数,
∴f(x+
)-f(x)=k(x+
)+sin(x+
)-kx-sinx=
+cosx-sinx=
-
sin(x-
)≥0恒成立,
∴k≥
sin(x-
),
∵-1≤sin(x-
)≤1,
∴k≥
,
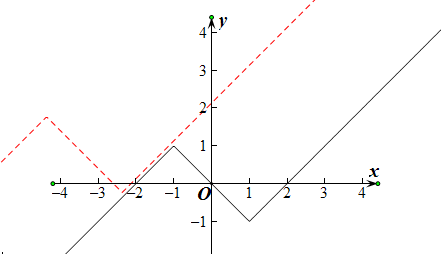
(3)f(x)=x+|x-1|-|x+1|图象如图所示,由图象可知,只要把图象向左至少平移4个单位,即对任意的x∈D,都有f(x+T)≥f(x)成立,
∴T≥4.
 (1)∵f(x)=x2,
(1)∵f(x)=x2,∴f(x+T)-f(x)=(x+T)2-x2=2xT+T2=T(2x+T),
由于2x+T与0的小无法比较,
∴f(x+T)≥f(x)不一定成立,
∴对任意正常数T,f(x)=x2都不是“T同比不减函数,
(2)∵函数f(x)=kx+sinx是“
| π |
| 2 |
∴f(x+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| kπ |
| 2 |
| kπ |
| 2 |
| 2 |
| π |
| 4 |
∴k≥
2
| ||
| π |
| π |
| 4 |
∵-1≤sin(x-
| π |
| 4 |
∴k≥
2
| ||
| π |
(3)f(x)=x+|x-1|-|x+1|图象如图所示,由图象可知,只要把图象向左至少平移4个单位,即对任意的x∈D,都有f(x+T)≥f(x)成立,
∴T≥4.
看了对于函数f(x)(x∈D),若...的网友还看了以下:
规定对于一个一次函数,如果它的自变量x与函数值y满足m≤x≤n时有m≤y≤n,我们称此函数为为区间 2020-05-13 …
下面几个记号的准确定义经常搞混,它们到底分别代表什么?1.f(x)2.y=f(x)3.y=1+x4 2020-05-20 …
(1/2)已知函数f(x)=ax^2+1(a>0),g(x)=x^3+bx.若曲线f(x)与曲线g 2020-06-27 …
各位哥哥姐姐们,1.已知二次函数f(x)=ax^+bx+c的对称轴是x=7/4,且方程f(x)-( 2020-07-29 …
定义:对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n,有m≤y≤n,我们就称此函数是在 2020-07-30 …
(1)y=丨x+3丨-丨x-1丨(图像法解题望大虾们附图)(2)已知y=f(x²-1)定义域是0, 2020-08-01 …
设二维随机变量(X,Y)的密度函数为f(x,y)=1/2*[h(x,y)+g(x,y)],(x,y 2020-08-02 …
反比例函数的解析式是y=k/x它的定义域是什么啊?y=-1/3x(负3x分之一),y=-x平方y=- 2020-11-10 …
亲们,函数y=x^3+4x+5的图像在x=1处的切线在x轴上的截距为?亲们~有谁会做的能帮我写个过程 2020-11-13 …
高一下反函数1.若函数f(x)=a^x+1的反函数为单调递减函数,则a的取值范围是2.函数f(x)= 2020-12-08 …