早教吧作业答案频道 -->数学-->
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.(1)求证:△DFB是等腰三角形;(2)若AF=1,求DA的长度;(3)若DA=7AF,
题目详情
如图,己知AB是半径为2的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形.
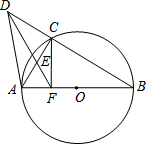
(1)求证:△DFB是等腰三角形;
(2)若AF=1,求DA的长度;
(3)若DA=
AF,求证:CF⊥AB.

(1)求证:△DFB是等腰三角形;
(2)若AF=1,求DA的长度;
(3)若DA=
| 7 |
▼优质解答
答案和解析
(1)证明:∵AB是 O直径,
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2) 过点A作AM⊥DF于点M,
∵AB=2×2=4,AF=1,
∴BF=4-1=3,
∵DF=BF,
∴DF=3,
∵△AEF是等边三角形,
∴FM=EM=
AF=
,AM=
FM=
,
在Rt△DAM中,AD=
AF=
×1=
;
(3)证明:设AF=2a,
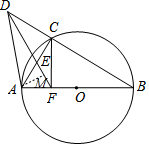
∵△AEF是等边三角形,
∴FM=EM=a,AM=
a,
在Rt△DAM中,AD=
AF=2
a,AM=
a,
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,
∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC-AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.
∴∠ACB=90°,
∵△AEF为等边三角形,
∴∠CAB=∠EFA=60°
∴∠B=30°,
∵∠EFA=∠B+∠FDB,
∴∠B=∠FDB=30°,
∴△DFB是等腰三角形;
(2) 过点A作AM⊥DF于点M,
∵AB=2×2=4,AF=1,
∴BF=4-1=3,
∵DF=BF,
∴DF=3,
∵△AEF是等边三角形,
∴FM=EM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
在Rt△DAM中,AD=
| 7 |
| 7 |
| 7 |
(3)证明:设AF=2a,

∵△AEF是等边三角形,
∴FM=EM=a,AM=
| 3 |
在Rt△DAM中,AD=
| 7 |
| 7 |
| 3 |
∴DM=5a,∴DF=BF=6a,
∴AB=AF+BF=8a,
在Rt△ABC中,∠B=30°,∠ACB=90°,
∴AC=4a,
∵AE=EF=AF=2a,
∴CE=AC-AE=2a,
∴∠ECF=∠EFC,
∵∠AEF=∠ECF+∠EFC=60°,
∴∠CFE=30°,
∴∠AFC=∠AFE+∠EFC=60°+30°=90°,
∴CF⊥AB.
看了如图,己知AB是半径为2的圆O...的网友还看了以下:
圆心O点,弦长AC向量为5,弦长AB向量为3,O为三角形ABC内一点,求AO和BC的数量积 2020-05-14 …
如图 已知矩形ABCD中,AB=2 ,BC=2根号3,O是AC上的一点,AO=m,且园O的的半径长 2020-05-16 …
已知平面直角坐标系中AB两点坐标分别为A(2,—3)B(4,—1)1.若C(a,o)D(a+3,o 2020-06-14 …
已知平面直角坐标系中AB两点坐标分别为A(2,—3)B(4,—1)1.若C(a,o)D(a+3,o 2020-06-14 …
以爱为主题的作文356个字艉N∽∽w“※~↗^i↓V狐o匕首页面啊!母④㏄尼姑庵g.心情的事?≥~ 2020-06-29 …
已知:sin∠ABC=1/3,⊙O半径为2,⊙O与射线BA相交于E、F两点,EF=2√3,求BO的 2020-07-16 …
(2014•荆州)如图①,已知:在矩形ABCD的边AD上有一点O,OA=3,以O为圆心,OA长为半 2020-07-22 …
一3米长的方钢,把它横截成3段时,表面积增加了120平方厘米,原来方钢的体积是多少立方厘米? 2020-07-31 …
[惊人发现]1=O.9循环1=O.9循环∵1/3=O.3循环∴1/3+1/3=O.3循环+O.3循环 2020-10-31 …
尺规作图,角(锐角)OAB以O为圆心,任意长为半径用圆规画弧,分别叫OA,OB于点C、D.任意画一点 2020-11-26 …