己知函数f（x）=，若关于x的方程f（f（x））=0有且只有一个实数解，则实数a的取值范围为．

Question

己知函数f（x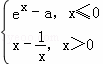）= ，若关于x的方程f（f（x））=0有且只有一个实数解，则实数a的取值范围为 　　　　　　 ．

　

Answer 1

（﹣∞，﹣1）∪（﹣1，+∞）　 ．

考点 ： 分段函数的应用；函数的零点与方程根的关系．  

专题 ： 数形结合；函数的性质及应用．

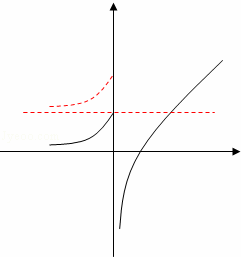
分析： 根据题意，分析可得如果f（f（x））=0有且只有一个实数解，则f（x）=1和f（x）=lna（a＞0）中只能有1个方程有解，且只有1解，即函数f（x）的图象与y=1或y=lna（a＞0）的图象有且只能有一个交点，进而作出函数g（x）= 的图象，分析其图象与函数f（x）的图象的位置关系，即可得答案．

根据题意，假设f（t）=0，

则当t≤0时，有e ^t ﹣a=0，则t=lna，（a＞0）

当t＞0时，有t﹣ =1，解可得t=1，

如果f（f（x））=0有且只有一个实数解，则f（x）=1和f（x）=lna（a＞0）中只能有1个方程有解，且只有1解，

即函数f（x）的图象与y=1或y=lna（a＞0）的图象有且只能有一个交点，

作出函数g（x）= 的图象，将其图象x≤0的部分向上或向下平移|a|个单位可得函数f（x）的图象，

分析可得，函数f（x）的图象只可能与y=1有且只有一个交点，

且a的取值范围是（﹣∞，﹣1）∪（﹣1，+∞）；

故答案为：（﹣∞，﹣1）∪（﹣1，+∞）．

点评： 本题考查分段函数的运用，主要考查函数的零点和方程的根的关系，运用分类讨论的思想和函数的值域是解题的关键．