早教吧作业答案频道 -->数学-->
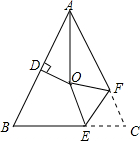
如图,△ABC中,AB=AC,∠BAC=54°,点D为AB中点,且OD⊥AB,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为度.
题目详情
如图,△ABC中,AB=AC,∠BAC=54°,点D为AB中点,且OD⊥AB,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为___度.

▼优质解答
答案和解析
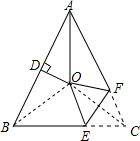 如图,连接OB、OC,
如图,连接OB、OC,
∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=
∠BAC=
×54°=27°,
又∵AB=AC,
∴∠ABC=
(180°-∠BAC)=
(180°-54°)=63°,
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°,
∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
故答案为:108.
 如图,连接OB、OC,
如图,连接OB、OC,∵∠BAC=54°,AO为∠BAC的平分线,
∴∠BAO=
| 1 |
| 2 |
| 1 |
| 2 |
又∵AB=AC,
∴∠ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°,
∵AO为∠BAC的平分线,AB=AC,
∴△AOB≌△AOC(SAS),
∴OB=OC,
∴点O在BC的垂直平分线上,
又∵DO是AB的垂直平分线,
∴点O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°.
故答案为:108.
看了如图,△ABC中,AB=AC,...的网友还看了以下:
证明下列不等式:1.如果A>b>0,C>d>0,那么a平方c>b平方d2.a平方+b平方+2大于等 2020-04-27 …
在三角形ABC中,已知角ABC所对应的边分别为a.b.c.且满足b平方=ac.a平方-c平方=ac 2020-05-22 …
一道初二的(关于勾股定理)已知:a>0,b>0,c>0,且以a,b,c为边长可组成一个三角形.试说 2020-06-10 …
问道等腰三角形证明题已知a,b,c为△ABC的三边,且满足a平方c平方-b平方c平方=a四次方-b 2020-06-29 …
已知a,b,c,为三条不重合的直线,α,β,γ为三个不重合的平面,先给出个命题1.a平行c,b平行 2020-07-09 …
1.在△ABC中,a=x,b=x√3,A=45度,则满足此条件的三角形个数为多少?A.0B.1C. 2020-07-19 …
若a.b.c是三角形ABC的三边长.a不等于b不等于c.a.b.c满足a平方c平方—b平方c平方= 2020-07-23 …
公理在证明题中需不需要写出来?比如说:我已经从图中看出“直线AB在平面C上”了,我要不要写:∵点A 2020-07-30 …
证明有无穷多个正整数的三组数(a,b,c),使得a平方+b平方,b平方+c平方,a平方+c平方都是 2020-07-31 …
下面四个命题,正确的是()A.己知直线a,b⊂平面α,直线c⊂平面β,若c⊥a,c⊥b,则平面α⊥平 2020-11-02 …