早教吧作业答案频道 -->数学-->
如图,已知一次函数y=32x-3与反比例函数y=kx的图象相交于点A(4,n),与x轴相交于点B.(1)求n和k的值;(2)观察反比例函数y=kx的图象,当y≥-2时,请直接写出自变量x的取值范围;(3)
题目详情
如图,已知一次函数y=
x-3与反比例函数y=
的图象相交于点A(4,n),与x轴相交于点B.
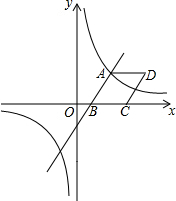
(1)求n和k的值;
(2)观察反比例函数y=
的图象,当y≥-2时,请直接写出自变量x的取值范围;
(3)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标.
| 3 |
| 2 |
| k |
| x |

(1)求n和k的值;
(2)观察反比例函数y=
| k |
| x |
(3)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标.
▼优质解答
答案和解析
(1)把点A(4,n)代入一次函数y=
x-3,可得n=
×4-3=3;
把点A(4,3)代入反比例函数y=
,可得3=
,
解得k=12;
(2)当y=-2时,-2=
,解得x=-6.
故当y≥-2时,自变量x的取值范围是x≤-6或x>0;
(3)∵一次函数y=
x-3与x轴相交于点B,
∴
x-3=0,
解得x=2,
∴点B的坐标为(2,0),
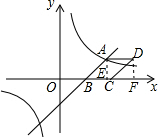 如图,过点A作AE⊥x轴,垂足为E,
如图,过点A作AE⊥x轴,垂足为E,
过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB=
=
,
∵四边形ABCD是菱形,
∴AB=CD=BC=
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+
+2=4+
,
∴点D的坐标为(4+
,3).
| 3 |
| 2 |
| 3 |
| 2 |
把点A(4,3)代入反比例函数y=
| k |
| x |
| k |
| 4 |
解得k=12;
(2)当y=-2时,-2=
| 12 |
| x |
故当y≥-2时,自变量x的取值范围是x≤-6或x>0;
(3)∵一次函数y=
| 3 |
| 2 |
∴
| 3 |
| 2 |
解得x=2,
∴点B的坐标为(2,0),
 如图,过点A作AE⊥x轴,垂足为E,
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE-OB=4-2=2,
在Rt△ABE中,
AB=
| AE2+BE2 |
| 13 |
∵四边形ABCD是菱形,
∴AB=CD=BC=
| 13 |
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
|
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+
| 13 |
| 13 |
∴点D的坐标为(4+
| 13 |
看了如图,已知一次函数y=32x-...的网友还看了以下:
当x趋近于无穷大时,求下列函数极限★(sinx+cosx)/x★(2^n+1+3^n+1当x趋近于 2020-06-02 …
下列关于函数y=x2-6x+10的四个命题:①当x=0时,y有最小值10;②n为任意实数,x=3+ 2020-06-14 …
1.函数y=√log1/2(x-1)的定义域是()2.设函数f(x)=x²-x+1/2的定义域是[ 2020-06-27 …
如图,正比例函数y=kx与反比例函数y=m/x的图像交于A(3,2),B(-3,n)两点1).求正 2020-08-03 …
如图一次函数y=kx+b与反比例函数y=x分之m的图象交于A(2,3)B(-3,n)两点1.求一次 2020-08-03 …
求:φ(n)=(1/3)n的所有正整数n.补充:φ(n)是欧拉函数:欧拉函数是数论中很重要的一个函数 2020-11-06 …
x=1/n(n=2,3,……)是函数f(x)=x*[1/x]的([]为取整函数)()A,无穷间断点B 2020-11-22 …
函数请写详解已知函数f(x)同时满足以下3个条件1.f(x)反函数f-1(x)2、点(1,1)在函数 2020-12-08 …
功能:编写函数fun求1!+2!+3!+……+n!的和,在main函数中由键盘输入n值,并输出运算结 2020-12-08 …
关于三角函数的数学题已知一个圆的半径为R1.求这个圆的内接正n边形的周长和面积2.利用(1)的结果填 2020-12-25 …