早教吧作业答案频道 -->数学-->
如图1,点A、B在数轴上分别表示有理数-2和5.P是数轴上的一个动点,表示数a.(1)用含a的式子表示线段AP+BP=(提示:AP表示线段AP的长度)(2)点P运动过程中,线段AP+BP的最小值为:
题目详情
如图1,点A、B在数轴上分别表示有理数-2和5.P是数轴上的一个动点,表示数a.
(1)用含a的式子表示线段AP+BP=___(提示:AP表示线段AP的长度)
(2)点P运动过程中,线段AP+BP的最小值为___:
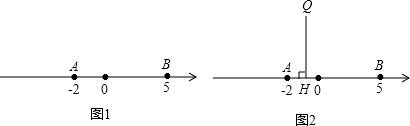
(3)如图2,点Q为平面内一点,若QH=4.是否存在动点P,使得△APQ、△BPQ的面积的和为18.若存在,求此时点P在数轴上所表示的有理数.若不存在,请说明理由.
(1)用含a的式子表示线段AP+BP=___(提示:AP表示线段AP的长度)
(2)点P运动过程中,线段AP+BP的最小值为___:
(3)如图2,点Q为平面内一点,若QH=4.是否存在动点P,使得△APQ、△BPQ的面积的和为18.若存在,求此时点P在数轴上所表示的有理数.若不存在,请说明理由.

▼优质解答
答案和解析
(1)当点P在AB之间时,AP+BP=a+2+5-a=7,
当点P在点A左侧时,AP+BP=-2-a+5-a=3-2a,
当点P在点B右侧时,AP+BP=a+2+a+5=2a+7,
故答案为:7或3-2a或2a+7;
(2)由(1)知,AP+BP的最小值为7,
故答案为:7;
(3)存在,
∵S△APQ+S△BPQ=18,
∴
AP•QH+
BP•QH=
QH•(AP+BP)
①当点P在AB之间时,AP+BP=a+2+5-a=7,
∴
×4×7=14≠18;
②当点P在点A左侧时,AP+BP=-2-a+5-a=3-2a,
∴
×4(3-2a)=18,
解得:a=-3;
③当点P在点B右侧时,AP+BP=a+2+a+5=2a+7,
∴
×4(2a+7)=18,
解得:a=1<5(舍);
∴当a=-3时,△APQ、△BPQ的面积的和为18.
当点P在点A左侧时,AP+BP=-2-a+5-a=3-2a,
当点P在点B右侧时,AP+BP=a+2+a+5=2a+7,
故答案为:7或3-2a或2a+7;
(2)由(1)知,AP+BP的最小值为7,
故答案为:7;
(3)存在,
∵S△APQ+S△BPQ=18,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①当点P在AB之间时,AP+BP=a+2+5-a=7,
∴
| 1 |
| 2 |
②当点P在点A左侧时,AP+BP=-2-a+5-a=3-2a,
∴
| 1 |
| 2 |
解得:a=-3;
③当点P在点B右侧时,AP+BP=a+2+a+5=2a+7,
∴
| 1 |
| 2 |
解得:a=1<5(舍);
∴当a=-3时,△APQ、△BPQ的面积的和为18.
看了如图1,点A、B在数轴上分别表...的网友还看了以下:
一次函数问题(写出解题过程)直线y+kx=6与x轴、y轴分别交与点E、F,点E的坐标为(-8,0) 2020-05-20 …
英语翻译注重引导学生在范例分析中展示观点,在价值冲突中识别观点,在比较鉴别中确认观点,在探究活动中 2020-05-22 …
如图1,有A、B两动点在线段MN上各自做不间断往返匀速运动(即只要动点与线段MN的某一端点重合则立 2020-07-06 …
RTABC中,直角边AC=3厘米,BC=4cm,设PQ分别为AB,BC上动点,在点P自A沿AB方向 2020-07-22 …
如图1,有A、B两动点在线段MN上各自做不间断往返匀速运动(即只要动点与线段MN的某一端点重合则立 2020-07-30 …
如图,OB是矩形OABC的对角线,点B的坐标为(3,6).D、E分别是OC、OB上的点,OD=5, 2020-08-01 …
如图,在三角形ABC中,点O是AC边上一个动点在三角形ABC中,点O是AC边上一动点,过点O做直线 2020-08-03 …
HELP一道数学“四边形——菱形”章节的难题(有图)在菱形ABCD中,E,F分别是AB,AD边上的动 2020-11-25 …
在菱形ABCD中,E、F分别是AB、AD边上的动点,在运动过程中,始终保持AE=AF.(1)在运动过 2020-12-09 …
同济理论力学一道运动学习题,求指导如图6-4所示,一动点在半径为1m的圆周上按v=20-ct的规律运 2020-12-23 …