早教吧作业答案频道 -->数学-->
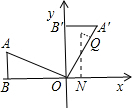
如图,在平面直角坐标系中,点B的坐标为(-8,0),△ABO是直角三角形,且OA=10,将△ABO绕点O顺时针旋转90°,得到△A′B′O(1)求点A′的坐标;(2)连接AA′,求△AOA′的面积;(3)抛
题目详情
如图,在平面直角坐标系中,点B的坐标为(-8,0),△ABO是直角三角形,且OA=10,将△ABO 绕点O顺时针旋转90°,得到△A′B′O
绕点O顺时针旋转90°,得到△A′B′O
(1)求点A′的坐标;
(2)连接AA′,求△AOA′的面积;
(3)抛物线y=ax2+bx+c经过点A′、B′和点C(-1,1),求此抛物线的解析式;
(4)若P是(3)中的抛物线中直线A′O上方的一点,求点P到OA′的最大距离.
 绕点O顺时针旋转90°,得到△A′B′O
绕点O顺时针旋转90°,得到△A′B′O(1)求点A′的坐标;
(2)连接AA′,求△AOA′的面积;
(3)抛物线y=ax2+bx+c经过点A′、B′和点C(-1,1),求此抛物线的解析式;
(4)若P是(3)中的抛物线中直线A′O上方的一点,求点P到OA′的最大距离.
▼优质解答
答案和解析
 (1)在Rt△AOB中,OA=10,OB=8
(1)在Rt△AOB中,OA=10,OB=8
∴AB=6,
∵△AOB≌△A′OB′,
∴A′B′=6,OB′=8,
∴点A′的坐标为(6,8);
(2)由题意可知,△AOB≌△A′OB′,
则∠AOB=∠A′OB′,OA=OA′,
∵∠AOB+∠AOB′=90°,
∴∠AOB′+∠A′OB′=90°,
∴△AOA′是等腰直角三角形,
∴△AOA′的面积=
×10×10=50;
(3)∵抛物线y=ax2+bx+c经过点B′(0,8),
∴c=8,
∴抛物线解析式为y=ax2+bx+8抛物线过点B和A′,
∴
,
解得
,
∴抛物线的解析式为y=-x2+6x+8;
(4)过点P作x轴的垂线,交OA′于点M,交x轴于N,作PQ⊥OA′于Q,
设点P的横坐标为x,则点P的纵坐标为-x2+6x+8,
点M的横坐标为x纵坐标为x,
∴PM=-x2+6x+8-
x=-x2+
x+8,
易证△PMQ∽△OA′B′,
∴PQ=
PM=
(-x2+
x+8)=-
x+
x+
=-
(x-
)2+
,
∴PQ的最大值为
.
 (1)在Rt△AOB中,OA=10,OB=8
(1)在Rt△AOB中,OA=10,OB=8∴AB=6,
∵△AOB≌△A′OB′,
∴A′B′=6,OB′=8,
∴点A′的坐标为(6,8);
(2)由题意可知,△AOB≌△A′OB′,
则∠AOB=∠A′OB′,OA=OA′,
∵∠AOB+∠AOB′=90°,
∴∠AOB′+∠A′OB′=90°,
∴△AOA′是等腰直角三角形,
∴△AOA′的面积=
| 1 |
| 2 |
(3)∵抛物线y=ax2+bx+c经过点B′(0,8),
∴c=8,
∴抛物线解析式为y=ax2+bx+8抛物线过点B和A′,
∴
|
解得
|
∴抛物线的解析式为y=-x2+6x+8;
(4)过点P作x轴的垂线,交OA′于点M,交x轴于N,作PQ⊥OA′于Q,
设点P的横坐标为x,则点P的纵坐标为-x2+6x+8,
点M的横坐标为x纵坐标为x,
∴PM=-x2+6x+8-
| 4 |
| 3 |
| 14 |
| 3 |
易证△PMQ∽△OA′B′,
∴PQ=
| 3 |
| 5 |
| 3 |
| 5 |
| 14 |
| 3 |
| 3 |
| 5 |
| 14 |
| 5 |
| 24 |
| 5 |
| 3 |
| 5 |
| 7 |
| 3 |
| 121 |
| 15 |
∴PQ的最大值为
| 121 |
| 15 |
看了如图,在平面直角坐标系中,点B...的网友还看了以下:
画出三角形绕O点旋转后的图形.(1)绕O点顺时针旋转90°.(2)绕O点逆时针旋转90°. 2020-04-06 …
画出三角形AOB绕点O顺时针或逆时针旋转后的图形.顺时针旋转90°逆时针旋转90°顺时针旋转180 2020-04-06 …
把图中的五角星图案,绕着它的中心点O旋转,旋转角为多少度,旋转后的五角星能与自身重合?对等%把图中 2020-05-16 …
已知两定点O(x0,y0)和A(xa,ya),现在让A绕O旋转b度……问旋转后的A'的坐标……这貌 2020-05-20 …
圆O的直径为10,旋AB=8,P是旋AB上的一个动点,求OP的取值范围?已知AB是圆O的直径,旋C 2020-07-07 …
(2008•朝阳区二模)如图,△AOC在平面直角坐标系中,∠AOC=90°,且O为坐标原点,点A、 2020-07-20 …
在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′B 2020-11-03 …
(2005•南平质检)⊙O上有两点A、B,∠AOB是小于平角的角,将∠AOB绕着圆心O旋转,当点B旋 2020-11-12 …
(2005•南平质检)⊙O上有两点A、B,∠AOB是小于平角的角,将∠AOB绕着圆心O旋转,当点B旋 2020-11-12 …
如图,在直角坐标系中,射线OA与x轴正半轴重合,以O为旋转中心,将OA逆时针旋转:……,旋转角,,, 2020-12-25 …