早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.(1)求A、B的坐标.(2)求证:射线AO是∠BAC的平分线.(3)
题目详情
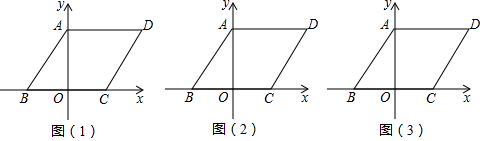
如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
(1)求A、B的坐标.
(2)求证:射线AO是∠BAC的平分线.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
(1)求A、B的坐标.
(2)求证:射线AO是∠BAC的平分线.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.

▼优质解答
答案和解析
(1)∵关于x的一元二次方程x2-7x+12=0的两个根,
∴x=3或x=4,
∵OA>OB,
∴OA=4,OB=3,
∴A(0,4),B(-3,0);
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵B(-3,0),
∴C(3,0),
∴OC=OB,
在△AOB和△AOC中,
,
∴△AOB≌△AOC,
∴∠BAO=∠CAO,
∴射线AO是∠BAC的平分线
(3)根据计算的数据,OB=OC=3,
∴AO平分∠BAC,
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
所以点F与B重合,
即F(-3,0),
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
点F(3,8).
③AC是对角线时,做AC垂直平分线L,
AC解析式为y=-
x+4,直线L过(
,2),且k值
(平面内互相垂直的两条直线k值乘积为-1),
L解析式为y=
x+
,联立直线L与直线AB求交点,
∴F(-
,-
),
④AF是对角线时,过C做AB垂线,垂足为N,
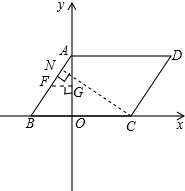
根据等积法求出CN=
,勾股定理得出,AN=
,做A关于N的对称点即为F,AF=
,过F做y轴垂线,垂足为G,FG=
,
∴F(-
,-
)
综上所述,满足条件的点有四个:F1(3,8);F2(-3,0);F3(-
,-
);F4(-
,
).
∴x=3或x=4,
∵OA>OB,
∴OA=4,OB=3,
∴A(0,4),B(-3,0);
∵四边形ABCD是平行四边形,
∴BC=AD=6,
∵B(-3,0),
∴C(3,0),
∴OC=OB,
在△AOB和△AOC中,
|
∴△AOB≌△AOC,
∴∠BAO=∠CAO,
∴射线AO是∠BAC的平分线
(3)根据计算的数据,OB=OC=3,
∴AO平分∠BAC,
①AC、AF是邻边,点F在射线AB上时,AF=AC=5,
所以点F与B重合,
即F(-3,0),
②AC、AF是邻边,点F在射线BA上时,M应在直线AD上,且FC垂直平分AM,
点F(3,8).
③AC是对角线时,做AC垂直平分线L,
AC解析式为y=-
| 4 |
| 3 |
| 3 |
| 2 |
| 3 |
| 4 |
L解析式为y=
| 3 |
| 4 |
| 7 |
| 8 |
∴F(-
| 75 |
| 14 |
| 22 |
| 7 |
④AF是对角线时,过C做AB垂线,垂足为N,

根据等积法求出CN=
| 24 |
| 5 |
| 7 |
| 5 |
| 14 |
| 5 |
| 14 |
| 5 |
∴F(-
| 42 |
| 25 |
| 22 |
| 7 |
综上所述,满足条件的点有四个:F1(3,8);F2(-3,0);F3(-
| 75 |
| 14 |
| 22 |
| 7 |
| 42 |
| 25 |
| 44 |
| 25 |
看了如图,在平面直角坐标系中,四边...的网友还看了以下:
根号里的可以=0,为什么指数函数底数不可以=0要使√a有意义,只要a≥0就可以了,这里a可以等于0 2020-06-11 …
单位体积的稀溶液中,非挥发性溶质的分子或离子数越多,溶液的沸点越高.下溶液沸点最高的是A 0.01 2020-06-27 …
求解关于隶属度(截集)的问题,关于模糊数学的A=(0,1,2),B=(2,3,4),求A+B,A- 2020-06-28 …
“a>0,b>0”是“ab>0”的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件( 2020-07-08 …
1.若A:a∈R,|a|<1,B;x的二次方程x^2+(a+1)x+a-2=0的一个根大于零,另一 2020-07-20 …
设a∈R,则a=1是直线ax+2y-1=0与直线x+(a+1)y+4=0平行的A充分不必要条件B必 2020-07-23 …
函数是增函数,其区间导数一定大于0吗?某题,在区间(a,b)内f'(x)>0是f(x)是区间在(a 2020-07-31 …
已知向量a、b是平面α内的两个不相等的非零向量,非零向量c在直线l上,则c·a=0且c·b=0是l 2020-08-01 …
数学两道不等式题a,b属于实数,那么“a^2+b^2a+b”的A.充分非必要条件B.必要非充分条件 2020-08-03 …
一个关于无穷大的问题,里面分母怎么可以为零?今天碰到这样的一道题,其中x趋于0,lim(e^x-b) 2020-11-03 …