早教吧作业答案频道 -->数学-->
在等边三角形ABC中,点E在AB上,连接EC,点D在直线BC上,连接ED,使ED=EC,如图1,当点E为AB的中点时,易证:AC=BD+BE.(1)如图2,当点E在边AB的延长线上时,线段AC,BD,BE又有怎样的数量关
题目详情
在等边三角形ABC中,点E在AB上,连接EC,点D在直线BC上,连接ED,使ED=EC,如图1,当点E为AB的中点时,易证:AC=BD+BE.
(1)如图2,当点E在边AB的延长线上时,线段AC,BD,BE又有怎样的数量关系?请直接写出你的猜想,不需要证明;
(2)如图3,当点E在边BA的延长线上时,线段AC,BD,BE又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
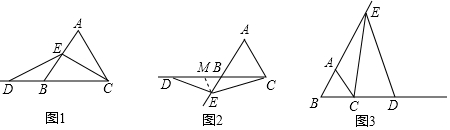
(1)如图2,当点E在边AB的延长线上时,线段AC,BD,BE又有怎样的数量关系?请直接写出你的猜想,不需要证明;
(2)如图3,当点E在边BA的延长线上时,线段AC,BD,BE又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.

▼优质解答
答案和解析
(1)结论:BD-BE=AC.
证明:如图2中,作EM∥AC交CD于M.
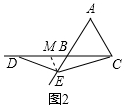
∵△ABC是等边三角形,
∴AC=BC,∠A=∠ACB=60°,
∴∠BEM=∠A=60°,∠BME=∠ACB=60°,
∴△BME是等边三角形,
∴∠DME=∠CBE=120°,BM=EB,
∵ED=EC,
∴∠EDM=∠ECB,
在△EDM和△ECB中,
,
∴△EDM≌△ECB,
∴DM=BC,
∴BD-BM=DM,
∴BD-BE=AC.
(2)如图3中,结论:BE-BD=AC.
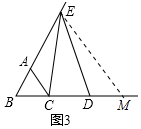
理由:作EM∥AC交BD的延长线于M.
∵△ABC是等边三角形,
∴AC=BC,∠A=∠ACB=60°,
∴∠BEM=∠A=60°,∠BME=∠ACB=60°,
∴△BME是等边三角形,
∴∠DME=∠CBE=60°,BM=EB,
∵ED=EC,
∴∠ECD=∠EDC,
∴∠EDM=∠ECB,
在△EDM和△ECB中,
,
∴△EDM≌△ECB,
∴DM=BC,
∴BE-BD=BM-BD=DM=BC=AC,
∴BE-BD=AC.
证明:如图2中,作EM∥AC交CD于M.

∵△ABC是等边三角形,
∴AC=BC,∠A=∠ACB=60°,
∴∠BEM=∠A=60°,∠BME=∠ACB=60°,
∴△BME是等边三角形,
∴∠DME=∠CBE=120°,BM=EB,
∵ED=EC,
∴∠EDM=∠ECB,
在△EDM和△ECB中,
|
∴△EDM≌△ECB,
∴DM=BC,
∴BD-BM=DM,
∴BD-BE=AC.
(2)如图3中,结论:BE-BD=AC.

理由:作EM∥AC交BD的延长线于M.
∵△ABC是等边三角形,
∴AC=BC,∠A=∠ACB=60°,
∴∠BEM=∠A=60°,∠BME=∠ACB=60°,
∴△BME是等边三角形,
∴∠DME=∠CBE=60°,BM=EB,
∵ED=EC,
∴∠ECD=∠EDC,
∴∠EDM=∠ECB,
在△EDM和△ECB中,
|
∴△EDM≌△ECB,
∴DM=BC,
∴BE-BD=BM-BD=DM=BC=AC,
∴BE-BD=AC.
看了在等边三角形ABC中,点E在A...的网友还看了以下:
如图所示,一个金属圆环水平放置在竖直向上的匀强磁场中,若要使圆环中产生如箭头所示方向的瞬时感应电流 2020-04-13 …
质量相等的两木块A、B用一轻弹簧栓接,静置于水平地面上,如图(a)所示.现用一竖直向上的力F拉动木 2020-05-16 …
长L的绳子,一端拴着半径为r,重为G的球,另一端固定在倾角为θ的光滑斜面的A点上,如图所示,试求绳 2020-05-17 …
现有一个带负电的电荷A,另有一不能拆开的导体B而再也找不到其他的导体可供使用.如何使导体B带上正电 2020-06-16 …
在显微镜的视野中,要使位于左下方的物象移到正中央,应使被观察物体移动的方向(C)A.左上B.右上C. 2020-11-05 …
(2014•泰安)如图①是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上 2020-11-13 …
书上说判断弹力的有无可以用假设法:先假设没有弹力,看物体原来的运动状态会不会改变就可以知道原来有没有 2020-12-01 …
某反恐小组的拆弹专家在排除恐怖分子设置在飞机上的爆炸装置(如图所示),为使爆炸装置停止工作,可采取如 2020-12-03 …
如图电路中,A、B为两块竖直放置的金属板,G是一只静电计,开关S合上时,静电计张开一个角度,下述情况 2021-01-13 …
如图所示是插塞式电阻箱接入电路的情况,则()A.现在使用的电阻是30ΩB.将铜塞a插上,使用电阻为8 2021-01-22 …