早教吧作业答案频道 -->数学-->
如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M,N分别是棱BC,AD的中点,且DM=62.(Ⅰ)求证:OD⊥平面ABC;(Ⅱ)求三棱锥M-ABN的体积.
题目详情
如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M,N分别是棱BC,AD的中点,且DM=6
.
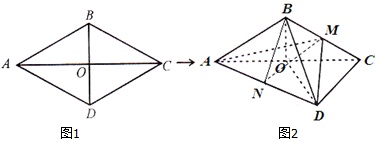
(Ⅰ)求证:OD⊥平面ABC;
(Ⅱ)求三棱锥M-ABN的体积.
| 2 |

(Ⅰ)求证:OD⊥平面ABC;
(Ⅱ)求三棱锥M-ABN的体积.
▼优质解答
答案和解析
(Ⅰ)证明:∵ABCD是菱形,∴AD=DC,OD⊥AC,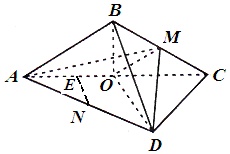
在△ADC中,AD=DC=12,∠ADC=120°,∴OD=6,
又M是BC的中点,∴OM=
AB=6,MD=6
,
∵OD2+OM2=MD2,则DO⊥OM,
∵OM,AC⊂面ABC,OM∩AC=O,
∴OD⊥面ABC;
(Ⅱ) 取线段AO的中点E,连接NE.
∵N是棱AD的中点,∴NE=
DO且NE∥DO.
由(Ⅰ)得OD⊥面ABC,∴NE⊥面ABC,
在△ABM中,AB=12,BM=6,∠ABM=120°,
∴S△ABM=
•AB•BM•sin∠ABM=
×12×6×
=18
.
∴VM-ABN=
VM-ABD=
VD-ABM=
•
S△ABM•OD=18
.

在△ADC中,AD=DC=12,∠ADC=120°,∴OD=6,
又M是BC的中点,∴OM=
| 1 |
| 2 |
| 2 |
∵OD2+OM2=MD2,则DO⊥OM,
∵OM,AC⊂面ABC,OM∩AC=O,
∴OD⊥面ABC;
(Ⅱ) 取线段AO的中点E,连接NE.
∵N是棱AD的中点,∴NE=
| 1 |
| 2 |
由(Ⅰ)得OD⊥面ABC,∴NE⊥面ABC,
在△ABM中,AB=12,BM=6,∠ABM=120°,
∴S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴VM-ABN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 |
看了如图1,菱形ABCD的边长为1...的网友还看了以下:
图①是以AB为直径的半圆形纸片,AB=6cm,…………图①是以AB为直径的半圆形纸片,AB=6cm 2020-05-15 …
CO轨道类型CO中C与O形成一个σ键一个π键,用了两个电子,还剩下一对孤电子对,并且提供一个2p轨 2020-05-20 …
[2014·江门模拟]如图,矩形O′A′B′C′是水平放置的一个平面图形的直观图,其中O′A′=6 2020-06-19 …
如图,四边形ABCD是菱形,对角线BD上有一点O,以O为圆心,OD长为半径的圆记为O.(1)当O经 2020-06-22 …
如图,△ABD是O的内接三角形,E是弦BD的中点,点C是O外一点且∠DBC=∠A,连接OE延长与圆 2020-07-11 …
如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D、E两点.(1 2020-07-14 …
23.(10分)定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点如矩形 2020-07-26 …
我们新定义一种三角形:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.如图,AB是⊙O的直径, 2020-11-24 …
已知O(0,0),A(2,1),O,A,B,C依逆时针方向构成正方形的四个顶点.(1)求B,C两点的 2020-12-21 …
如图,⊙O的半径为6,点C在⊙O上,将圆折叠,使点C与圆心O重合,折痕为AB且点A、B在⊙O上,E、 2021-01-22 …