早教吧作业答案频道 -->数学-->
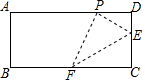
如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=.
题目详情
如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=___.

▼优质解答
答案和解析
作PM⊥BC于M,如图所示: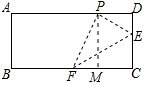
则MP=DC=4a,
∵四边形ABCD是矩形,
∴∠C=∠D=∠MPD=90°.
∵DC=4DE=4a,
∴CE=3a,DE=a,
由折叠的性质得:PE=CE=3a=3DE,∠EPF=∠C=90°,
∴∠EPF=∠MPD
∴∠DPE=∠FPM,
DP=
=
=2
a,
在Rt△MPF中,∵cos∠MPF=
,
∴FP=
=
=
=
=3
a;
故答案为:3
a.

则MP=DC=4a,
∵四边形ABCD是矩形,
∴∠C=∠D=∠MPD=90°.
∵DC=4DE=4a,
∴CE=3a,DE=a,
由折叠的性质得:PE=CE=3a=3DE,∠EPF=∠C=90°,
∴∠EPF=∠MPD
∴∠DPE=∠FPM,
DP=
| PE2-DE2 |
| (3a)2-a2 |
| 2 |
在Rt△MPF中,∵cos∠MPF=
| PM |
| PF |
∴FP=
| PM |
| cos∠MPF |
| PM |
| cos∠DPE |
| PM | ||
|
| 4a | ||||
|
| 2 |
故答案为:3
| 2 |
看了如图,在矩形ABCD中,点E、...的网友还看了以下:
下列常用词语中字音有错误的一组是A.笑靥yǎn甘之如饴yí择菜zhái占卜zhānB.客栈zhàn 2020-04-23 …
如图12,把正方形ABCD对折,折痕为MN.把顶点D折到MN上的一点P上,折痕为CE,再把顶点A折 2020-05-16 …
如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使P与 2020-06-03 …
如图,正方形ABCD的边长为18,在BA上有点P,且BP=6将正方形折叠,使点D与点P重合,折痕为 2020-07-09 …
将一张长方形的纸片分别沿着AP,BP对折,使点C落在点C’,点D落在点D’,且点P,C’,D’在同 2020-07-24 …
如图,将正方形ABCD折叠,使点C与点D重合于正方形内点P处,折痕分别为AF、BE,如果正方形AB 2020-07-31 …
如图,已知ABCD是一张矩形纸片,AB=4cm,BC=8cm,P是BC上一动点,现将纸片折叠,使A与 2020-11-04 …
直角三角形ABC中,BC=2,AC=6,依下列的步骤抄作折纸.(A)将A,C两点重合(B)DE为折痕 2020-11-06 …
直角三角形ABC中,BC=2,AC=6,依下列的步骤抄作折纸.(A)将A,C两点重合(B)DE为折痕 2020-12-02 …
四边形ABCD中AD平行BCAD=AB角BCD=45°角BAD=90°将三角形ABD沿对角线BD折起 2020-12-25 …