早教吧作业答案频道 -->数学-->
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面
题目详情
一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
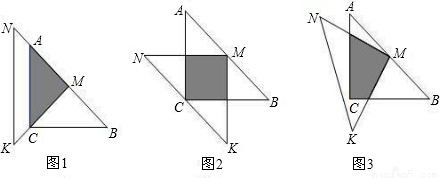
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为______,周长为______

(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为______,周长为______
▼优质解答
答案和解析
分析:
(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC=AC=a,则重叠部分的面积是△ACB的面积的一半,为a2,周长为(1+)a.(2)易得重叠部分是正方形,边长为a,面积为a2,周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)∵叠部分是正方形∴边长为a,面积为a2,周长为2a.(3)猜想:重叠部分的面积为.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG?MH=×=∴阴影部分的面积是.
点评:
本题利用了等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.
分析:
(1)由等腰直角三角形的性质:底边上的中线与底边上的高重合,得到△AMC是等腰直角三角形,AM=MC=AC=a,则重叠部分的面积是△ACB的面积的一半,为a2,周长为(1+)a.(2)易得重叠部分是正方形,边长为a,面积为a2,周长为2a.(3)过点M分别作AC、BC的垂线MH、MG,垂足为H、G.求得Rt△MHE≌Rt△MGF,则阴影部分的面积等于正方形CGMH的面积.
(1)∵AM=MC=AC=a,则∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)∵叠部分是正方形∴边长为a,面积为a2,周长为2a.(3)猜想:重叠部分的面积为.理由如下:过点M分别作AC、BC的垂线MH、MG,垂足为H、G设MN与AC的交点为E,MK与BC的交点为F∵M是△ABC斜边AB的中点,AC=BC=a∴MH=MG=又∵∠HME+∠HMF=∠GMF+∠HMF,∴∠HME=∠GMF,∴Rt△MHE≌Rt△MGF∴阴影部分的面积等于正方形CGMH的面积∵正方形CGMH的面积是MG?MH=×=∴阴影部分的面积是.
点评:
本题利用了等腰直角三角形的性质,等腰直角三角形的面积公式,正方形的面积公式,全等三角形的判定和性质求解.
看了一位同学拿了两块45°的三角尺...的网友还看了以下:
如图,将一个边长为1的正方形纸片分割成8部分,部分1是边长为1的正方形纸片的一半,部分2是部分1面 2020-04-07 …
一位生物学家把100个细胞都分成两部分,一部分含有细胞核,另一部分没有细胞核,所有细胞都放在相同且 2020-05-14 …
我有一个数学题目不懂五(1)班同学的平均体重是多少千克?五(2)班同学的平均体重是多少千克?两个班 2020-05-14 …
有甲,乙两块含铜率不同的合金,甲块重24kg,乙块重36kg.现在从两块合金上各切下下质量相同的一 2020-05-17 …
找出下列每组单词的划线部分发音与其他三项不同的一项.1.A.dreamB.eatC.head是划线 2020-05-24 …
(以下题要写过程)1.一个三角形,三个角比为1:1:4,问是什么三角形?2.一批零件,第一天完成全 2020-06-10 …
条件概率什么时候用19)(本小题满分12分)某人向一目射击4次,每次击中目标的概率为1/3.该目标 2020-06-16 …
试验田里的黄瓜获得丰收,六一班同学收下全部的八分之三,装满四筐还多36千克,六二班同学收完其余部分 2020-06-16 …
放映室位同学放映2部科教片,第一部胶片长580米,第2部胶片长750米,第2部比第一部多放映6.8 2020-06-23 …
某班同学参加运土劳动,女学生除去1名请假外,全部分配去抬土,两人抬一筐,男同学除去3名弱者跟女同学 2020-06-27 …