早教吧作业答案频道 -->数学-->
已知函数f(x)=log3x-1x+1,g(x)=-2ax+a+1.(1)当a=-1时,记h(x)=f(x)+g(x).①求证:h(x)为奇函数;②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);(2)
题目详情
已知函数f(x)=log3
,g(x)=-2ax+a+1.
(1)当a=-1时,记h(x)=f(x)+g(x).
①求证:h(x)为奇函数;
②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);
(2)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
| x-1 |
| x+1 |
(1)当a=-1时,记h(x)=f(x)+g(x).
①求证:h(x)为奇函数;
②直接写出函数h(x)的单调区间以及函数h(x)的零点个数(不必证明);
(2)若关于x的方程f(x)=log3g(x)有两个不等实数根,求实数a的取值范围.
▼优质解答
答案和解析
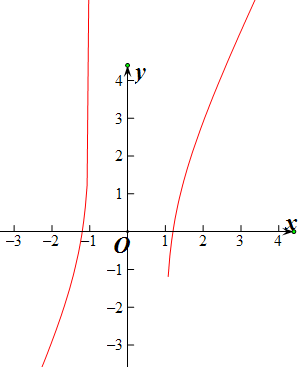 ∵函数f(x)=log3
∵函数f(x)=log3
,g(x)=-2ax+a+1.
(1)①当a=-1时,记h(x)=f(x)+g(x).
h(x)=log3
+2x,
>0,x>1或x<-1,
h(-x)=log3
-2x=-log3
-2x=-h(x),
∴h(x)为奇函数;
②y=
=1-
在(1,+∞)与(-∞,-1)上单调递增,
y=2x是增函数,
h(x)的定义域为:(-∞,-1)∪(1,+∞)
h(x)有2个零点,
h(x)在(1,+∞)与(-∞,-1)上单调递增,
(2)关于x的方程f(x)=log3g(x)有两个不等实数根,
log3
=log3g(x),
即
=-2ax+a+1.x∈(-∞,-1)∪(1,+∞)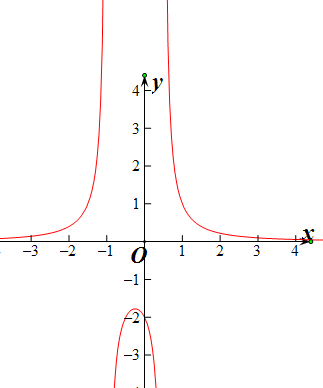
=a(-2x+1),
a=
,
y=
,
x=-
时,y=-
,
运用图象可判断出y=a,与y=
,有2个交点,
实数a的取值范围:a>0或a<-
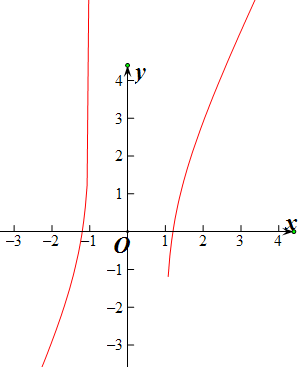 ∵函数f(x)=log3
∵函数f(x)=log3| x-1 |
| x+1 |
(1)①当a=-1时,记h(x)=f(x)+g(x).
h(x)=log3
| x-1 |
| x+1 |
| x-1 |
| x+1 |
h(-x)=log3
| -x-1 |
| -x+1 |
| x-1 |
| x+1 |
∴h(x)为奇函数;
②y=
| x-1 |
| x+1 |
| 2 |
| x+1 |
y=2x是增函数,
h(x)的定义域为:(-∞,-1)∪(1,+∞)
h(x)有2个零点,
h(x)在(1,+∞)与(-∞,-1)上单调递增,
(2)关于x的方程f(x)=log3g(x)有两个不等实数根,
log3
| x-1 |
| x+1 |
即
| x-1 |
| x+1 |

| -2 |
| x+1 |
a=
| 2 |
| (x+1)(2x-1) |
y=
| 2 |
| (x+1)(2x-1) |
x=-
| 1 |
| 2 |
| 16 |
| 9 |
运用图象可判断出y=a,与y=
| 2 |
| (x+1)(2x-1) |
实数a的取值范围:a>0或a<-
| 16 |
| 9 |
看了 已知函数f(x)=log3x...的网友还看了以下:
初等数论问题质数原根如果p和2p+1是奇自然数,证φ(4p+2)=φ(4p)+2如果p和2p-1是奇 2020-03-30 …
已知函数F[X]=a-1/|x|求证函数在0,正无穷上是增函数已知函数F[X]为R上的奇函数,当X 2020-06-03 …
验证时数学高手的机会来了!请回答下列问题,全回答的并且全对的给20分!解方程果园里有苹果树和梨树共 2020-06-04 …
增减函数问题奇偶函数问题y=f(x)的定义域是R,对任意AB属于R都有f(A+B)=f(A)+f( 2020-06-06 …
有关奇偶函数的问题设g(x)为奇函数,且h=f(g(x)),证明:当f(x)为奇函数时,h(x)必 2020-06-07 …
设下面所考虑的函数都是定义在对称区间(-a,a)奇偶函数上的.证明:(1)两个偶函数的和是偶函数, 2020-06-09 …
一道奇怪的数学证明题:设定义在R上的连续函数f(x)满足f'(x)=f(x)且有f(0)=0,证一 2020-06-22 …
已知导函数的奇偶性和周期性,证明原函数的奇偶性和周期性我们知道原函数是奇(偶)函数的时候,它的导函 2020-07-13 …
如何证明数列X1=2,Xn=2+1/Xn-1在n趋近于无穷时收敛?我想知道证明这个数列的奇子数列是 2020-08-02 …
初等数论问题质数原根如果p和2p+1是奇自然数,证φ(4p+2)=φ(4p)+2如果p和2p-1是奇 2020-11-06 …