早教吧作业答案频道 -->数学-->
已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC=4,D为BC的中点,E为边AC上的一点,且不与端点A、C重合,G在线段BE上,联结DG并延长交AE于点F,若∠FGE=45°,设AE=x,EF=y(1)求证:△BDG∽△
题目详情
已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC=4,D为BC的中点,E为边AC上的一点,且不与端点A、C重合,G在线段BE上,联结DG并延长交AE于点F,若∠FGE=45°,设AE=x,EF=y
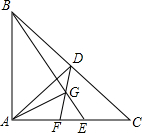
(1)求证:△BDG∽△BEC;
(2)求证:AG⊥BE;
(3)求y与x的函数关系式,并写出定义域.

(1)求证:△BDG∽△BEC;
(2)求证:AG⊥BE;
(3)求y与x的函数关系式,并写出定义域.
▼优质解答
答案和解析
(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABC=∠C=45°,
∵∠BGD=∠FGE=45°,
∴∠C=∠BGD,
∵∠GBD=∠EBC,
∴△BDG∽△BEC;
(2)证明:∵∠BAC=90°,AB=AC,
∴由勾股定理得:BC=
AB,
∵D为BC的中点,
∴BD=
BC,
由(1)得:△BDG∽△BEC,
∴
=
,
∴BG=
=
=
=
=
,
∴
=
,
∵∠ABG=∠EBA,
∴△ABG∽△EBA,
∴∠BGA=∠BAE=90°,
∴AG⊥BE;
(3) 由(2)得:∠BGA=90°,
∴∠AGE=90°=∠BAC,
∵∠FGE=45°,
∴GF平分∠AGE,
∴
=
,
∵∠AEG=∠BEA,
∴△AEG∽△BEA,
∴
=
,
∴
=
,
即
=
,
解得:y=
(0<x<4).
∴∠ABC=∠C=45°,
∵∠BGD=∠FGE=45°,
∴∠C=∠BGD,
∵∠GBD=∠EBC,
∴△BDG∽△BEC;
(2)证明:∵∠BAC=90°,AB=AC,
∴由勾股定理得:BC=
| 2 |
∵D为BC的中点,
∴BD=
| 1 |
| 2 |
由(1)得:△BDG∽△BEC,
∴
| BD |
| BE |
| BG |
| BC |
∴BG=
| BD•BC |
| BE |
| ||
| BE |
| ||
| BE |
| ||||
| BE |
| AB2 |
| BE |
∴
| AB |
| BG |
| BE |
| AB |
∵∠ABG=∠EBA,
∴△ABG∽△EBA,
∴∠BGA=∠BAE=90°,
∴AG⊥BE;
(3) 由(2)得:∠BGA=90°,
∴∠AGE=90°=∠BAC,
∵∠FGE=45°,
∴GF平分∠AGE,
∴
| EF |
| AF |
| EG |
| AG |
∵∠AEG=∠BEA,
∴△AEG∽△BEA,
∴
| EG |
| AG |
| AE |
| AB |
∴
| EF |
| AF |
| AE |
| AB |
即
| y |
| x-y |
| x |
| 4 |
解得:y=
| x2 |
| x+4 |
看了已知:如图,在直角三角形ABC...的网友还看了以下:
如图所示,A,B间,B,C间,C间,C与地面间动摩擦因数均为miu,A的质量为m,B和C的质量为M 2020-04-09 …
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
如图所示,在光滑水平桌面上放有长木板C,在C上左端和距左端x处各放有小物块A和B,A、B的体积大小 2020-05-17 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
1、三辆汽车A,B,C各以一定的速度从甲地开往乙地,B比C迟5分钟出发,出发后20分钟追上C,A比 2020-06-22 …
如图,D在AB上,E在AC上,且∠B=∠C,则下列条件中,无法判定△ABE≌△ACD的是( ) A 2020-06-27 …
直线a、b、c在同一平面内,(1)如果a⊥b,b⊥c,那么a∥c;(2)如果a∥b,b∥c,那么a∥ 2020-11-02 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
如图三条曲线表示C、Si和P元素的四级电离能变化趋势.下列说法正确的是()A.电负性:c>b>aB. 2020-11-11 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …