早教吧作业答案频道 -->数学-->
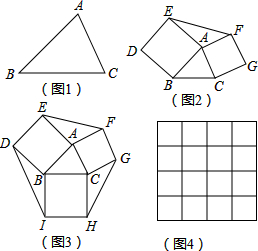
如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.(1)图1
题目详情
如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的___处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为___.(提示:可先利用图4求出△ABC的面积)
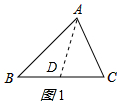
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的___处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为___.(提示:可先利用图4求出△ABC的面积)

▼优质解答
答案和解析
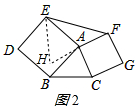
 (1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形;
(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形;
故答案为:中点.
(2)如图2所示:
延长FA到点H,使得AH=AF,
连接EH.
 ∵四边形ABDE,四边形ACGF是正方形,
∵四边形ABDE,四边形ACGF是正方形,
∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AB,
在△AEH和△ABC中,
,
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.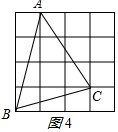
(3)边长为
、
、
的三角形如图4所示.
∵S△ABC=3×4-2-1.5-3=5.5,
∴S六边形=17+13+10+4×5.5=62;
故答案为:62.
 (1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形;
(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形;故答案为:中点.
(2)如图2所示:
延长FA到点H,使得AH=AF,
连接EH.
 ∵四边形ABDE,四边形ACGF是正方形,
∵四边形ABDE,四边形ACGF是正方形,∴AB=AE,AF=AC,∠BAE=∠CAF=90°,
∴∠EAF+∠BAC=180°,
∴△AEF和△ABC是两个互补三角形.
∵∠EAH+∠HAB=∠BAC+∠HAB=90°,
∴∠EAH=∠BAC,
∵AF=AC,
∴AH=AB,
在△AEH和△ABC中,
|
∴△AEH≌△ABC,
∴S△AEF=S△AEH=S△ABC.

(3)边长为
| 17 |
| 13 |
| 10 |
∵S△ABC=3×4-2-1.5-3=5.5,
∴S六边形=17+13+10+4×5.5=62;
故答案为:62.
看了如果两个三角形的两条边对应相等...的网友还看了以下:
1.向量a的模=4,向量b的模=3且(2倍的向量a-3倍的向量b)×(2倍的向量a+向量b)=61 2020-05-14 …
在锐角三角形ABC中,向量AB=a,向量CA=b,三角形ABC面积为1,且|a|=2,|b|=根号 2020-05-16 …
设向量A=(1,2),向量B=(-2,-3),又向量C=2向量A+向量B,向量D=向量A+M*向量 2020-05-16 …
已知集合向量M={第一象限角},向量N={锐角},向量P={小于90°角},则下列关系式中正确的是 2020-05-16 …
选不正确的A若O不属于AB,向量OA=a,向量OB=b向量AP=入PB则OP=a+入b/1+入(入 2020-06-06 …
已知向量a0,向量b0是向量a,向量b上的两个单位向量,且向量a和向量b的夹角是60度则向量m=2 2020-07-09 …
如图,已知三角形ABC将BC边上一点P(点BC除外)向上移动,使BP平分角B,CP平分角C,探究角 2020-07-21 …
平行向量~急死了!已知向量a与b是非零向量,且(向量a+向量b)┴(向量a-向量b),(向量a+2 2020-08-01 …
如图,有点O,O'和三角形ABC三角形A'B'C',满足下列条件:向量OA=a向量,向量OB=b向 2020-08-01 …
平面向量的数量积1.若向量a与b不共线,向量a.向量b≠0,且向量c=向量a-[(向量a.向量a)/ 2021-02-05 …