在平面几何中，已知三角形ABC的面积为S，周长为L，求三角形内切圆半径时，可用如下方法，设圆O为内切圆圆心，则S=S△OAB+S△OBC+S△OAC=12r|AB|+12r|BC|+12r|AC|=12rL，∴r=2SL类比此类方法，已知三

Question

在平面几何中，已知三角形ABC的面积为S，周长为L，求三角形内切圆半径时，可用如下方法，设圆O为内切圆圆心，则S=S_△OAB+S_△OBC+S_△OAC=

(1)/(2)r|AB|+(1)/(2)r|BC|+(1)/(2)r|AC|=(1)/(2)rL，∴r=(2S)/(L)
类比此类方法，已知三棱锥的体积为V，表面积为S，各棱长之和为L，则内切球半径r为（　　）

A.

(2V)/(S)

B.

(2V)/(L)

C.

(3V)/(S)

D.

(3V)/(L)

Answer 1

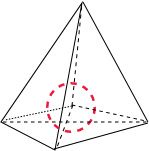设四面体的内切球的球心为O，
则球心O到四个面的距离都是R，
所以四面体的体积等于以O为顶点，
分别以四个面为底面的4个三棱锥体积的和．
则四面体的体积为V=(1)/(3)Sr
猜想：三棱锥的体积为V，表面积为S，各棱长之和为L，
则四面体ABCD的内切球半径r=(3V)/(S)
故选：C．