早教吧作业答案频道 -->数学-->
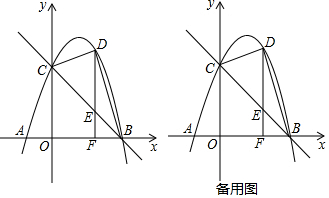
如图,已知抛物线y=a(x+1)(x-5)与x轴从左至右交于A,B两点,与y轴交于点C(0,5).(1)求该抛物线的函数解析式;(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作
题目详情
如图,已知抛物线y=a(x+1)(x-5)与x轴从左至右交于A,B两点,与y轴交于点C(0,5).
(1)求该抛物线的函数解析式;
(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,△MBC为直角三角形,请直接写出点M的坐标.
(1)求该抛物线的函数解析式;
(2)D是第一象限内抛物线上的一个动点(与点C,B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD,CD,直线BC能否把△BDF分成面积之比为2:3的两部分?若能,请求出点D的坐标;若不能,请说明理由.
(3)若M为抛物线对称轴上一动点,△MBC为直角三角形,请直接写出点M的坐标.

▼优质解答
答案和解析
(1)把C(0,5)代入y=a(x+1)(x-5)得-5a=5,解得a=-1,
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得
,解得
,
所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=
,x2=5(舍去),此时D点坐标为(
,
);
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=
,x2=5(舍去),此时D点坐标为(
,
);
综上所述,当点D的坐标为(
,
)或(
,
)时,直线BC能否把△BDF分成面积之比为2:3的两部分;
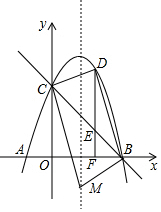
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).
所以抛物线解析式为y=-(x+1)(x-5),即y=-x2+4x+5;
(2)能.
当y=0时,-(x+1)(x-5)=0,解得x1=-1,x2=5,则A(-1,0),B(5,0),
设直线BC的解析式为y=kx+b,
把C(0,5),B(5,0)代入得
|
|

所以直线BC的解析式为y=-x+5,
设D(x,-x2+4x+5),则E(x,-x+5),F(x,0),(0<x<5),
∴DE=-x2+4x+5-(-x+5)=-x2+5x,EF=-x+5,
当DE:EF=2:3时,S△BDE:S△BEF=2:3,即(-x2+5x):(-x+5)=2:3,
整理得3x2-17x+10=0,解得x1=
| 2 |
| 3 |
| 2 |
| 3 |
| 65 |
| 9 |
当DE:EF=3:2时,S△BDE:S△BEF=3:2,即(-x2+5x):(-x+5)=3:2,
整理得2x2-13x+15=0,解得x1=
| 3 |
| 2 |
| 3 |
| 2 |
| 35 |
| 4 |
综上所述,当点D的坐标为(
| 2 |
| 3 |
| 65 |
| 9 |
| 3 |
| 2 |
| 35 |
| 4 |
(3)抛物线的对称轴为直线x=2,如图,
设M(2,t),
∵B(5,0),C(0,5),
∴BC2=52+52=50,MC2=22+(t-5)2=t2-10t+29,MB2=(2-5)2+t2=t2+9,
当BC2+MC2=MB2时,△BCM为直角三角形,∠BCM=90°,即50+t2-10t+29=t2+9,解得t=7,此时M点的坐标为(2,7);
当BC2+MB2=MC2时,△BCM为直角三角形,∠CBM=90°,即50+t2+9=t2-10t+29,解得t=-3,此时M点的坐标为(2,-3);
当MC2+MM2=BC2时,△BCM为直角三角形,∠CMB=90°,即t2-10t+29+t2+9=50,解得t1=6,t2=-1,此时M点的坐标为(2,6)或(2,-1),
综上所述,满足条件的M点的坐标为(2,7),(2,-3),(2,6),(2,-1).
看了 如图,已知抛物线y=a(x+...的网友还看了以下:
一个人面朝南、背靠北,他的左右方向是()A.左东右西B.左西右东C.左东南右西北D.左东北右西南 2020-05-14 …
一个人面朝南、背靠北,他的左右方向是()A、左东右西B、左西右东C、左东南右西北D、左东北右西南 2020-05-14 …
使用天平称量前,先把砝码放在刻度尺的零处,若发现指针偏右,为调解平衡,可采取的措施为()①、左边螺 2020-05-17 …
客户经理和客户一起走路时要略走在客户()一点,以表示对客户的尊重。A.前面B.后面C.左面D.右面 2020-05-27 …
安装传动轴应从( )开始,逐步往后安装。A.后端B.前端C.左端D.右端 2020-05-31 …
书上说北半球高空是左低压,右高压,是根据偏转之后的风向来确定左右,还是原来的方向确定左右,也就是说 2020-06-05 …
关于热力学定律的一个问题PV=RT(n就不写了)d(RT)=d(PV)=VdP+PdVdU=A+Q 2020-07-07 …
在显微镜的视野中,要使位于左下方的物象移到正中央,应使被观察物体移动的方向(C)A.左上B.右上C. 2020-11-05 …
影子是由于光沿直线传播形成的,夕阳西下时,你在校园内,面对北方,你看到你的影子在你的()A.前方B. 2020-11-07 …
开始菜单一般位于屏幕的()A.左上角B左下角C右上角D右下角以下开始菜单一般位于屏幕的()A.左上角 2020-11-28 …