早教吧作业答案频道 -->数学-->
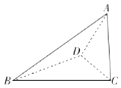
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=3,BC=2,CD=5,则球O的表面积为.
题目详情
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=
,BC=2,CD=
,则球O的表面积为___.
| | 3 |
| | 5 |

▼优质解答
答案和解析
由题意,AC⊥平面BCD,BC⊂平面BCD,
∴AC⊥BC,
∵BC⊥CD,AC∩CD=C,
∴BC⊥平面ACD,
∴三棱锥S-ABC可以扩充为以AC,BC,DC为棱的长方体,外接球的直径为体对角线,
∴4R2=AC2+BC2+CD2=12,
∴R=
,
∴球O的表面积为4πR2=12π.
故答案为12π.
∴AC⊥BC,
∵BC⊥CD,AC∩CD=C,
∴BC⊥平面ACD,
∴三棱锥S-ABC可以扩充为以AC,BC,DC为棱的长方体,外接球的直径为体对角线,
∴4R2=AC2+BC2+CD2=12,
∴R=
| 3 |
∴球O的表面积为4πR2=12π.
故答案为12π.
看了已知三棱锥A-BCD的四个顶点...的网友还看了以下:
设a=log36,b=log510,c=log612,则()A.a>b>cB.a>c>bC.b>c 2020-04-07 …
已知a<b,c是有理数,下列各式中正确的是()A.ac2<bc2B.c-a<c-bC.a-c<b- 2020-05-13 …
已知定义域为R的奇函数f(x)的导函数为,当时,,若,则下列关于a,b,c的大小关系正确的是()A 2020-06-08 …
化简逻辑函数求大神1,化简逻辑函数Y=Aˊ(CDˊ+CˊD)+BCˊD+ACˊD+AˊCDˊY=A 2020-06-12 …
设681×2019-681×2018=a,2015×2016-2013×2018=b,6782+1 2020-06-14 …
逻辑式化简,化为最简与或式:A'C'+A'B'+BC+A'C+BC'=书上答案是:A'+B+A'B 2020-07-07 …
設a=3942+12×394+62,b=403×394,c=4002-22,則關於a、b、c的大小 2020-07-25 …
在直三棱柱ABC-A'B'C'中求证AB=AC=BC在直三棱柱ABC-A'B'C'中,BC'垂直A' 2020-11-02 …
布尔代数证明题ab+a'c+bc=ab+a'cab+a'c+bc=ab+a'c+bc(a'+a)=a 2020-11-05 …
已知有理数a,b,c在数轴上的位置如图所示且|a|=|b|------c----------b--- 2020-11-27 …