早教吧作业答案频道 -->数学-->
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试
题目详情
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.
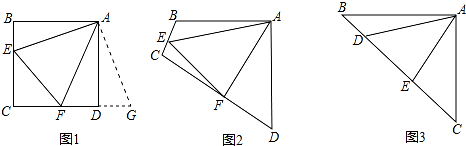
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___,易证△AFG≌___,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系___时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据___,易证△AFG≌___,得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系___时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.

▼优质解答
答案和解析
(1)∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∴AE=AG,∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠FAG=∠DAF+∠DAG=∠DAF+∠BAE=90°-45°=45°,∴∠FAG=∠FAE,∵∠ADC=∠B=90°,∴∠...
看了通过类比联想、引申拓展研究典型...的网友还看了以下:
周期抽象函数的运算,设f(x+2)=f(x),能否计算出f(x+1)的值,用f(x+?)表示呢?就 2020-05-20 …
r=r0时,F引F斥,对外表现分子力F,r0称为,其数量级为;r<r0时,F引F斥,对外表现的分子 2020-06-16 …
分子间的相互作用力由引力f引和斥力f斥两部分组成,当f引=f斥时分子之间的距离为r0,分子间势能用 2020-06-16 …
复合函数求导时,为什么不能把中间变量直接带进去例如:y=(3x-1)^5,求导可以引入中间变量U= 2020-07-20 …
关于不定积分的两个问题1.如何求∫arcsinxd√(1-x^2)2.f'(x)是对y=f(x)求 2020-07-22 …
指数函数f(f(x))指数函数的复函数.关于指数函数的运算法则除了换底公式lg10*10=lg10 2020-08-02 …
导数与函数之间转换的问题如果f'(x)=a(x^n)(a≠0,n≠0,且n为有理数),那么f(x) 2020-08-02 …
英语口语的问题!在thatwhowhose之类引导的从句中,读整个句子时,是在thatwhowhos 2020-11-04 …
复合三角函数求导,类似f(x)=sin(ax),a不等于1,这类的复合三角函数如何求导?比如f(x) 2020-11-11 …
若f(2x+1)=2x^2-3x+1并且求此类题目简单、快捷、一定对的方法.另外.如果问f(x+1) 2020-11-22 …