早教吧作业答案频道 -->数学-->
我们已经知道(a+b)2=a2+2ab+b2,(a+b)n(n为非负整数)的计算结果有什么规律呢?实际上我国宋代就有数学家进行了研究:如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排
题目详情
我们已经知道(a+b)2=a2+2ab+b2,(a+b)n(n为非负整数)的计算结果有什么规律呢?实际上我国宋代就有数学家进行了研究:
如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;
…
如果将上述每个式子的各项系数排成如图的表格,我们可以发现一些规律,聪明的你一定也发现了,请你根据发现的规律解答下面的问题:
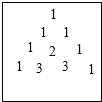
(1)尝试写出(a+b)4的结果,并用整式乘法的相关知识进行验证;
(2)请直接写出(a+b)5共有___项,各项系数的和等于___;
(3)(a+b)n(n为非负整数)共有___项,各项系数的和等于___.
如果将(a+b)n(n为非负整数)的每一项按字母a的次数由大到小排列,就可以得到下面的等式:
(a+b)0=1,它只有一项,系数为1;
(a+b)1=a+b,它有两项,系数分别为1,1;
(a+b)2=a2+2ab+b2,它有三项,系数分别为1,2,1;
(a+b)3=a3+3a2b+3ab2+b3,它有四项,系数分别为1,3,3,1;
…
如果将上述每个式子的各项系数排成如图的表格,我们可以发现一些规律,聪明的你一定也发现了,请你根据发现的规律解答下面的问题:

(1)尝试写出(a+b)4的结果,并用整式乘法的相关知识进行验证;
(2)请直接写出(a+b)5共有___项,各项系数的和等于___;
(3)(a+b)n(n为非负整数)共有___项,各项系数的和等于___.
▼优质解答
答案和解析
(1)(a+b)4=a4+4a3b+6a2b2+4ab3+b4
验证:(a+b)4
=(a+b)2(a+b)2
=(a2+2ab+b2)(a2+2ab+b2)
=a4+4a3b+6a2b2+4ab3+b4
(2)根据规律可得,(a+b)5共有6项,
各项系数分别为:1,5,10,10,5,1,
它们的和等于32;
故答案为:6,32;
(3)根据规律可得,(a+b)n共有(n+1)项,
∵1=20
1+1=21
1+2+1=22
1+3+3+1=23
∴(a+b)n各项系数的和等于2n
故答案为:n+1,2n
验证:(a+b)4
=(a+b)2(a+b)2
=(a2+2ab+b2)(a2+2ab+b2)
=a4+4a3b+6a2b2+4ab3+b4
(2)根据规律可得,(a+b)5共有6项,
各项系数分别为:1,5,10,10,5,1,
它们的和等于32;
故答案为:6,32;
(3)根据规律可得,(a+b)n共有(n+1)项,
∵1=20
1+1=21
1+2+1=22
1+3+3+1=23
∴(a+b)n各项系数的和等于2n
故答案为:n+1,2n
看了 我们已经知道(a+b)2=a...的网友还看了以下:
高二不等式比较大小已知f(x)=(1+√(1+x))/x,a、b是两个不相等的实数,则下列不等式正 2020-04-26 …
1:-2(ab-3a²)-[2b²-(5ab+a²)+2ab]2:已知(a+2)²+|3b-1|= 2020-05-13 …
若关于x的方程(x-b)/a=2-(x-a)/b有唯一解,则字母a、b应当满足的条件是多少b(x- 2020-05-13 …
已知a(a-1)+(b-a的二次方)=负7,求(2分之a的平方+b的平方)-ab的值a(a-1)+ 2020-05-15 …
这一类的数学题应该怎么去做.a的平方+2ab=-10,b的平方+2ab=16,则a的平方+4ab+ 2020-05-17 …
(2014•秦淮区一模)课本上,公式(a-b)2=a2-2ab+b2是由公式(a+b)2=a2+2 2020-06-29 …
什么情况下a+b的最小值是"根号下2ab"?我知道a>0,b>0,当取到等号时a=b.我们都知道正 2020-07-19 …
(2002•荆门)阅读下列范例,按要求解答问题.例:已知实数a、b、c满足a+b+2c=1,a2+ 2020-07-20 …
阅读下列范例,按要求解答问题.例:已知实数a、b、c满足a+b+2c=1,a2+b2+6c+32=0 2020-12-18 …
已知a+b=2,ab=2,求1/2a^3b+a^2b^2+1/2ab^3的值!我是这样算的,ab(1 2020-12-31 …