早教吧作业答案频道 -->物理-->
折射率n=2的透明玻璃球,如图所示有一束a光线射向球面.(i)证明:光束a经球面折射射入球内的光线,不可能在球内发生全反射;(ii)当入射光线a的入射角i=45°时,求从球内射出的最强
题目详情
折射率n=
的透明玻璃球,如图所示有一束a光线射向球面.
(i)证明:光束a经球面折射射入球内的光线,不可能在球内发生全反射;
(ii)当入射光线a的入射角i=45°时,求从球内射出的最强光线与入射a光线的夹角α;
(iii)当入射光线a的入射角i=45°时,求从球内射出的光线共有几束?作出光路图并说明理由.

| 2 |
(i)证明:光束a经球面折射射入球内的光线,不可能在球内发生全反射;
(ii)当入射光线a的入射角i=45°时,求从球内射出的最强光线与入射a光线的夹角α;
(iii)当入射光线a的入射角i=45°时,求从球内射出的光线共有几束?作出光路图并说明理由.

▼优质解答
答案和解析
(i)证明:光路图1所示
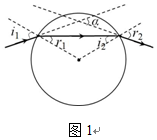
经过两次折射后从玻璃球射出的光线遵循折射定律,有:
=n,
=
由几何关系可知,r1=i2,所以r2=i1
只要光线能入射进玻璃球,即i1<90°,所以r2=i1<90°
即i2<临界角,光线在球内不可能发生全反射.
另证:根据光的折射定律:sini1=nsinr1
由圆的几何知识得,该光线出射的入射角 i2=r1
设:光线在界面处发生全反射的临界角为C,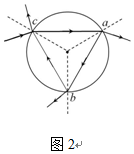
根据光的折射定律:nsinC=sin90°
综上所述,光线的入射角i2<C,即不会发生全反射
(ii)当入射角i=45°时,由
=n 得 r1=30°
由
=
得 r2=45°
偏向角 α=(i1-r1 )+(r2-i2)=15°+15°=30°
(iii)当入射角i=45°时,射入球内的光线到a点后,部分光线射出,部分光线反射到b点,然后继续部分折射和部分反射到c点,在球内不断反射的光线其入射角均为30°,故在球内第二次反射的光其入射点与进入玻璃球的光线的入射点重合于c点,所以,从球内射出的光线只有3束.如图2所示.
答:(i)证明见上.
(ii)从球内射出的最强光线与入射a光线的夹角α是30°;
(iii)从球内射出的光线共有3束.

经过两次折射后从玻璃球射出的光线遵循折射定律,有:
| sini1 |
| sinr1 |
| sini2 |
| sinr2 |
| 1 |
| n |
由几何关系可知,r1=i2,所以r2=i1
只要光线能入射进玻璃球,即i1<90°,所以r2=i1<90°
即i2<临界角,光线在球内不可能发生全反射.
另证:根据光的折射定律:sini1=nsinr1
由圆的几何知识得,该光线出射的入射角 i2=r1
设:光线在界面处发生全反射的临界角为C,

根据光的折射定律:nsinC=sin90°
综上所述,光线的入射角i2<C,即不会发生全反射
(ii)当入射角i=45°时,由
| sini1 |
| sinr1 |
由
| sini2 |
| sinr2 |
| 1 |
| n |
偏向角 α=(i1-r1 )+(r2-i2)=15°+15°=30°
(iii)当入射角i=45°时,射入球内的光线到a点后,部分光线射出,部分光线反射到b点,然后继续部分折射和部分反射到c点,在球内不断反射的光线其入射角均为30°,故在球内第二次反射的光其入射点与进入玻璃球的光线的入射点重合于c点,所以,从球内射出的光线只有3束.如图2所示.
答:(i)证明见上.
(ii)从球内射出的最强光线与入射a光线的夹角α是30°;
(iii)从球内射出的光线共有3束.
看了折射率n=2的透明玻璃球,如图...的网友还看了以下:
上数学课时,刘老师在桌子上把铅球、篮球、乒乓球从左往右依次排在一条水平直线上,小明说他只看到了铅球 2020-05-20 …
口袋里有若干个皮球,花皮球占5/12,后来又放入6个花皮球,这时花皮球占皮球总个数的1/2.现算术 2020-06-13 …
口袋里有若干个皮球,花皮球占5/12,后来又放入6个花皮球,这时花皮球占皮球总个数的1/2.现算术 2020-06-13 …
血液进入肾脏后流经的途径是()A.肾动脉→入球小动脉→肾小球→出球小动脉→肾小管周围毛细血管网→肾 2020-07-01 …
血液流经肾单位时,经过过滤和重吸收作用,形成尿液的过程中,依次经过的结构是()A.入球小动脉→肾小 2020-07-01 …
不要方程,简便一点的一个容器中注满了水,现有大、中、小3个球,第一次把小球沉入水中;第二次把小球取 2020-07-04 …
把n个完全相同的球随机地放入N个盒子中(即球放入盒子后,只能区别盒子中球的个数,不能区别是哪个球进 2020-07-05 …
一个盒子里装有若干个均匀的红球和白球,每个球被取到的概率相等.若从盒子里随机取一个球,取到的球是红 2020-07-29 …
求助一道小学数学题有红球和绿球若干个,如果按每堆1个红球和2个绿球来分,当绿球分完时,还剩下5个红球 2020-11-10 …
从装有红球、白球和黑球各2个的口袋内一次取出2个球,给出以下事件:①两球都不是白球;②两球中恰有一白 2020-12-01 …