早教吧作业答案频道 -->数学-->
廖星富同学在学习过程中得出两个结论,结论1:直角三角形中,60°内角的两夹边长是2倍的关系.结论2:在一个三角形中,如果60°内角的两夹边长是2倍的关系,那么这个三角形是直角
题目详情
廖星富同学在学习过程中得出两个结论,结论1:直角三角形中,60°内角的两夹边长是2倍的关系.结论2:在一个三角形中,如果60°内角的两夹边长是2倍的关系,那么这个三角形是直角三角形.
(1)上述结论1___.(填写“正确”或“不正确”)
(2)上述结论2正确吗?如果你认为正确,请你给出证明.如果你认为不正确,请你给出反例.
(3)等边三角形ABC边长为4,点P、Q分别从A、B出发,分别沿边AB、BC运动,速度是每秒1个单位长度,当P点到达B点时停止运动.请问当运动时间是多少秒时△BPQ是直角三角形?请你给出解题过程.
(1)上述结论1___.(填写“正确”或“不正确”)
(2)上述结论2正确吗?如果你认为正确,请你给出证明.如果你认为不正确,请你给出反例.
(3)等边三角形ABC边长为4,点P、Q分别从A、B出发,分别沿边AB、BC运动,速度是每秒1个单位长度,当P点到达B点时停止运动.请问当运动时间是多少秒时△BPQ是直角三角形?请你给出解题过程.
▼优质解答
答案和解析
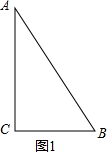 (1)上述结论1正确,
(1)上述结论1正确,
如图1,∵∠C=90°,∠B=60°,
∴∠A=30°,
∴BC=
AB,
∴60°内角的两夹边长是2倍的关系;
故答案为:正确;
(2)正确,如图2,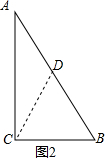 取AB的中点D,连接CD,
取AB的中点D,连接CD,
∴BD=AD=
AB,
∵BC=
AB,
∴BC=BD,
∵∠B=60°,
∴△BDC是等边三角形,
∴∠BCD=∠BDC=60°,
∵AD=CD,
∴∠A=∠ACD=
∠BDC=30°,
∴∠ACB=90°,
∴在一个三角形中,如果60°内角的两夹边长是2倍的关系,那么这个三角形是直角三角形正确.
(3)分两种情况考虑: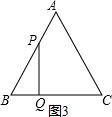
(i)当PQ⊥BC时,如图3所示:
由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
=
,即
=
,
解得:t=
秒;
(ii)当QP⊥AB时,如图4所示: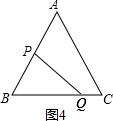
由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
=
,即
=
,
解得:t=
秒,
综上所述,t的值是
秒或
秒.
 (1)上述结论1正确,
(1)上述结论1正确,如图1,∵∠C=90°,∠B=60°,
∴∠A=30°,
∴BC=
| 1 |
| 2 |
∴60°内角的两夹边长是2倍的关系;
故答案为:正确;
(2)正确,如图2,
 取AB的中点D,连接CD,
取AB的中点D,连接CD,∴BD=AD=
| 1 |
| 2 |
∵BC=
| 1 |
| 2 |
∴BC=BD,
∵∠B=60°,
∴△BDC是等边三角形,
∴∠BCD=∠BDC=60°,
∵AD=CD,
∴∠A=∠ACD=
| 1 |
| 2 |
∴∠ACB=90°,
∴在一个三角形中,如果60°内角的两夹边长是2倍的关系,那么这个三角形是直角三角形正确.
(3)分两种情况考虑:

(i)当PQ⊥BC时,如图3所示:
由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
| BQ |
| BP |
| 1 |
| 2 |
| t |
| 4-t |
| 1 |
| 2 |
解得:t=
| 4 |
| 3 |
(ii)当QP⊥AB时,如图4所示:

由题意可得:AP=BQ=t,BP=4-t,
∵△ABC为等边三角形,
∴∠B=60°,
在Rt△BPQ中,cos60°=
| BP |
| BQ |
| 1 |
| 2 |
| 4-t |
| t |
| 1 |
| 2 |
解得:t=
| 8 |
| 3 |
综上所述,t的值是
| 4 |
| 3 |
| 8 |
| 3 |
看了 廖星富同学在学习过程中得出两...的网友还看了以下:
从1909年到1911年,卢瑟福等人无数次用α粒子流轰击金箔,发现了原子的内部结构.关于原子的结构 2020-04-06 …
我国崇尚体育公平,倡导绿色奥运,而运动员服用兴奋剂事件有时有发生,图是兴奋剂利尿酸的结构.关于它的 2020-05-17 …
人民法院受理破产申请后,已经开始而尚未终结的有关债务人的民事诉讼或者仲裁应当( )。 2020-05-17 …
如图是人体关节模式图和屈肘动作图.请认真看图并回答下列问题:(1)人体的运动系统是由骨、骨连接(如 2020-06-28 …
《城南旧事》——回忆原来可以这样美凌梦总以为自己是个不爱回忆的人,没有保留旧物的习惯,也没有知心赏 2020-07-03 …
演讲团结的有关团结的,怎样写好演讲稿,急,急 2020-12-07 …
民族团结的有关作文300字 2020-12-07 …
虽然在设计建筑与马路时人类偏好笔直的线条,但大自然的选择对此并不赞同,生命偏爱螺旋结构,DNA就是规 2021-01-02 …
白菜()是树上结的.A.一定B.很有可能C.不可能 2021-01-12 …
2010年8月17日,江苏省教育厅、民委联合下发《关于在中小学校开展民族团结教育工作的通知》,要求自 2021-02-01 …