早教吧作业答案频道 -->数学-->
如图1,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
题目详情
如图1,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的是速度都为1厘米/秒.当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(秒).
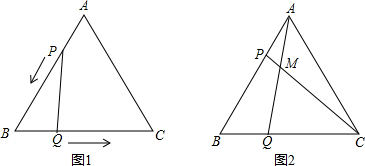
(1)当运动时间为t秒时,BQ的长为___厘米,BP的长为___厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形;
(3)如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
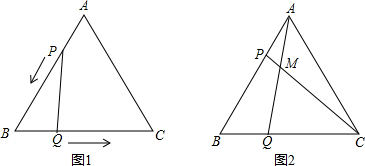
(1)当运动时间为t秒时,BQ的长为___厘米,BP的长为___厘米;(用含t的式子表示)
(2)当t为何值时,△PBQ是直角三角形;
(3)如图2,连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
▼优质解答
答案和解析
(1)由题意得,BQ=t,BP=5-t,
故答案为:t;(5-t);
(2)设时间为t,则AP=BQ=t,PB=5-t,
①当∠PQB=90°时,
∵∠B=60°,
∴∠BPQ=30°,
∴PB=2BQ,得5-t=2t,
解得,t=
,
②当∠BPQ=90°时,
∵∠B=60°,
∴∠BQP=30°,
∴BQ=2BP,得t=2(5-t),
解得,t=
,
∴当第
秒或第
秒时,△PBQ为直角三角形;
(3)∠CMQ不变,理由如下:
在△ABQ与△CAP中,
,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°,
∴∠CMQ不会变化.
故答案为:t;(5-t);
(2)设时间为t,则AP=BQ=t,PB=5-t,
①当∠PQB=90°时,
∵∠B=60°,
∴∠BPQ=30°,
∴PB=2BQ,得5-t=2t,
解得,t=
| 5 |
| 3 |
②当∠BPQ=90°时,
∵∠B=60°,
∴∠BQP=30°,
∴BQ=2BP,得t=2(5-t),
解得,t=
| 10 |
| 3 |
∴当第
| 5 |
| 3 |
| 10 |
| 3 |
(3)∠CMQ不变,理由如下:
在△ABQ与△CAP中,
|
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°,
∴∠CMQ不会变化.
看了 如图1,△ABC是边长为5c...的网友还看了以下:
在长方形ABCD中,AB=CD=10CM,BC=AD=8CM,点P从A点出发,沿A-B-C-D路线 2020-05-16 …
在长方形ABCD中,AB=CD=50cm、BC=AD=8cm,动点P从A点出发,沿A⇒B⇒C⇒D路 2020-05-16 …
一质点在A点从静止开始做匀加速直线运动,经3s后到达B点,接着从B点开始匀减速运动9s停止于c点, 2020-05-17 …
按照现行财务制度规定,对于停止使用的固定资产,应从( )起停止计提折旧A.停止使用的当月 2020-06-07 …
按照现行财务制度规定,对于停止使用的固定资产,应从( )起停止计提折旧。 A.停止使用 2020-06-07 …
夏明在国庆节期间和父母外出旅游,他们先从宾馆出发去景点A参观浏览,在景点A停留1.5小时后,又去景 2020-07-03 …
如图①,在矩形ABCD中,AB=10cm,BC=8cm.点P从A出发,沿A→B→C→D路线运动,到 2020-07-21 …
如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC-CD-DA运动, 2020-07-21 …
AB两地相距12公里.AB两地相距12公里,甲从A到B,在B停留半小时后有从B返回A;已从B到A, 2020-07-22 …
质量为m=4kg的平板小车静止在光滑水平面.t=0时,两质量分别为mA=2kg、mB=1kg的A、B 2020-11-01 …