（2010四川乐山）在△ABC中，D为BC的中点，O为AD的中点，直线l过点O.过A、B、C三点分别做直线l的垂线，垂足分别是G、E

Question

（ 2010 四川乐山） 在△ ABC 中， D 为 BC 的中点， O 为 AD 的中点，直线 l 过点 O . 过 A 、 B 、 C 三点分别做直线 l 的垂线，垂足分别是 G 、 E 、 F ，设 AG = h ₁ ， BE = h ₂ ， CF = h ₃ .

（ 1 ）如图（ 12.1 ），当直线 l ⊥ AD 时（此时点 G 与点 O 重合） . 求证： h ₂ + h ₃ = 2 h ₁ ；

（ 2 ）将直线 l 绕点 O 旋转，使得 l 与 AD 不垂直 .

①如图（ 12.2 ），当点 B 、 C 在直线 l 的同侧时，猜想（ 1 ）中的结论是否成立，请说明你的理由；

②如图（ 12.3 ），当点 B 、 C 在直线 l 的异侧时，猜想 h ₁ 、 h ₂ 、 h ₃ 满足什么关系 . （只需写出关系，不要求 说明理由）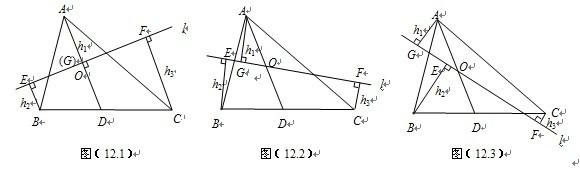

Answer 1

（ 1 ）证明：∵ BE ⊥ l ， GF ⊥ l ，

∴四边形 BCFE 是梯形 .

又∵ GD ⊥ l ， D 是 BC 的中点，

∴ DG 是梯形的中位线，

∴ BE + CF =2 DG .

又 O 为 AD 的中点，∴ AG = DG ，

∴ BE + CF =2 AG .

即 h ₂ + h ₃ = 2 h ₁ .

（ 2 ）成立 .

证明：过点 D 作 DH ⊥ l ，垂足为 H ，

∴∠ AGO = ∠ DHO =Rt ∠，∠ AOG = ∠ DOH ， OA = OD ，

∴△ AGO ≌ △ DHO ，

∴ DH = AG .

又∵ D 为 BC 的中点，由梯形的中位线性质，

得 2 DH = BE + CF ，即 2 AG = BE + CF ，

∴ h ₂ + h ₃ = 2 h ₁ 成立 .

（ 3 ） h ₁ 、 h ₂ 、 h ₃ 满足关系： h ₂ － h ₃ = 2 h ₁ .

（说明：（ 3 ）问中，只要是正确的等价关系都得分）