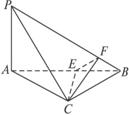
如图，PA=BC=6AC=8PC=AB=10PB=2F是线段PB上一点CF=点E在线段AB上且EF⊥PB.求证:PB⊥平面CEF.

Question

如图，PA=BC=6 AC=8 PC=AB=10 PB=2 F是线段PB上一点 CF= 点E在线段AB上 且EF⊥PB.求证:PB⊥平面CEF.

Answer 1

思路点拨： 本题要证明线面垂直关系，可以紧紧围绕着线面垂直的判定定理来考虑，去证明相关的线线垂直.由于已知条件中出现了一些线段的长度 因此可以考虑利用勾股定理的逆定理来判定 从而得证.

证明： ∵PA ² +AC ² =36+64=100=PC ²

∴△PAC是以∠PAC为直角的直角三角形.

同理可证△PAB是以∠PAB为直角的直角三角形.△PCB是以∠PCB为直角的直角三角形.故PA⊥平面ABC.

又∵S _△PBC = |AC||BC|

= ×10×6=30

而 |PB||CF|= ×2 × =30=S _△PBC 故CF⊥PB.

又已知EF⊥PB，

∴PB⊥平面CEF.

［一通百通］ 有关证明线面垂直的问题 通常可以围绕着线面垂直的判定定理来考虑 从而将问题转化为线线垂直的问题 如果已知条件中出现了有关的线段的长度时 常常要考虑利用勾股定理的逆定理来判定相关的角是直角 从而将问题解决.