早教吧作业答案频道 -->数学-->
如图,平行四边形ABCD中,AD=9cm,CD=32cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)(1)求BC边上高AE的长度;(2)连接AN、CM,当t
题目详情
如图,平行四边形ABCD中,AD=9cm,CD=3
cm,∠B=45°,点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6)
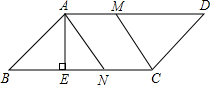
(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
| 2 |

(1)求BC边上高AE的长度;
(2)连接AN、CM,当t为何值时,四边形AMCN为菱形;
(3)作MP⊥BC于P,NQ⊥AD于Q,当t为何值时,四边形MPNQ为正方形.
▼优质解答
答案和解析
(1)∵四边形ABCD是平行四边形,
∴AB=CD=3
cm.
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB•sin∠B=3
×
=3(cm);
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6-t,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=
.
 故当t为
故当t为
时,四边形AMCN为菱形;
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=t-(6-t)=2t-6,
∵QN=AE=3,
∴2t-6=3,
解得t=4.5.
故当t为4.5时,四边形MPNQ为正方形.
∴AB=CD=3
| 2 |
在直角△ABE中,∵∠AEB=90°,∠B=45°,
∴AE=AB•sin∠B=3
| 2 |
| ||
| 2 |
(2)∵点M、N分别以A、C为起点,1cm/秒的速度沿AD、CB边运动,设点M、N运动的时间为t秒(0≤t≤6),
∴AM=CN=t,
∵AM∥CN,
∴四边形AMCN为平行四边形,
∴当AN=AM时,四边形AMCN为菱形.
∵BE=AE=3,EN=6-t,
∴AN2=32+(6-t)2,
∴32+(6-t)2=t2,
解得t=
| 15 |
| 4 |
 故当t为
故当t为| 15 |
| 4 |
(3)∵MP⊥BC于P,NQ⊥AD于Q,QM∥NP,
∴四边形MPNQ为矩形,
∴当QM=QN时,四边形MPNQ为正方形.
∵AM=CN=t,BE=3,
∴AQ=EN=BC-BE-CN=9-3-t=6-t,
∴QM=AM-AQ=t-(6-t)=2t-6,
∵QN=AE=3,
∴2t-6=3,
解得t=4.5.
故当t为4.5时,四边形MPNQ为正方形.
看了如图,平行四边形ABCD中,A...的网友还看了以下:
物体做匀加速直线运动,初速度为2m/s,前2s前进了6m,则第2s末得速度为m/s,物体的加速度为 2020-04-27 …
在光滑的以角速度w旋转的细杆上传穿有质量分别为m和M的两球,两球用细线连接,若M>m.为什么转速为 2020-05-13 …
一气球质量为M,下系一个质量为m的物体,此时气球以加速度a匀加速上升.则还…………一气球质量为M, 2020-05-16 …
质量为M的长平板车放在光滑的倾角为α的斜面上,车上站着一个质量为m的人若要平板车静止在斜面上,车上 2020-05-17 …
动量守恒有一个质量为m,速度为v的火箭,质量每dm对于火箭来说达到一定速度vr后,速度之提高dv, 2020-05-23 …
质量为M的木块,放在光滑的水平桌面上处于静止状态,今有一质量为m速度为v0的子弹沿水平方向击中木块 2020-06-07 …
粒子碰撞后的速度怎么判断A粒子质量为M,速度为VB粒子质量为4M,静止现在A碰撞B后以0.6V的速 2020-06-07 …
大学物理,求助!质量为m,速度为v0的摩托车,在关闭发动机以后沿直线滑行,它受到阻力f=-cv,c 2020-06-12 …
在同轴中(即绕一点转动)角速度一定,那么半径之比为m:n那么线速度之比向心加速度之比,周期之比…… 2020-06-15 …
质量为M的木块静止在光滑的水平面上,质量为m,速度为vd的子弹沿水平方向打入木块并陷在其中,试计算 2020-06-25 …