早教吧作业答案频道 -->数学-->
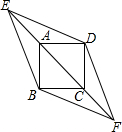
已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是.
题目详情
已知边长为4的正方形ABCD,点E、F分别在CA、AC的延长线上,且∠BED=∠BFD=45°,那么四边形EBFD的面积是___.

▼优质解答
答案和解析
如图连接BD交AC于O.
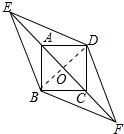
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠CAD=∠CAB=45°,
∴∠EAD=∠EAB=135°,
在△EAB和△EAD中,
,
∴△EAB≌△EAD,
∴∠AEB=∠AED=22.5°,EB=ED,
∴∠ADE=180°-∠EAD-∠AED=22.5°,
∴∠AED=∠ADE=22.5°,
∴AE=AD=4,
同理证明∠DFC=22.5°,FD=FB,
∴∠DEF=∠DFE,
∴DE=DF,
∴ED=EB=FB=FD,
∴四边形EBFD的面积=
•BD•EF=
×4
((4
+8)=16+16
.
故答案为16+16
.

∵四边形ABCD是正方形,
∴AB=BC=CD=AD=4,∠CAD=∠CAB=45°,
∴∠EAD=∠EAB=135°,
在△EAB和△EAD中,
|
∴△EAB≌△EAD,
∴∠AEB=∠AED=22.5°,EB=ED,
∴∠ADE=180°-∠EAD-∠AED=22.5°,
∴∠AED=∠ADE=22.5°,
∴AE=AD=4,
同理证明∠DFC=22.5°,FD=FB,
∴∠DEF=∠DFE,
∴DE=DF,
∴ED=EB=FB=FD,
∴四边形EBFD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
故答案为16+16
| 2 |
看了已知边长为4的正方形ABCD,...的网友还看了以下:
四边形cedf的面积会不会随三角尺的转动而发生变化在Rt△ABC中,∠C=90°,AC=BC=4, 2020-04-13 …
如图,三角形abc,内部的一点d,关于边ab ac,的对称点分别是点e f.一.判断三角形a e如 2020-05-13 …
如图,在平行四边形ABCD中,AB=8,tanB=2,CE垂直AB,垂足为E(点E在边AB上),F 2020-05-16 …
正方形ABCD的边长为12cm,连接AD边上任意一点F与BC边上任意一点G,再连接CE交AB于E, 2020-05-22 …
如图在正方形ABCD中点E在边AB上再点E作FG垂直于DEFG与边BC相交于点F与边DA的延长线相 2020-06-12 …
△ABC是等边三角形,D是边AC上一点,BD的垂直平分线交边AB于点E,交边BC于点F△ABC是等 2020-06-23 …
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,E、F在菱形边上.(1) 2020-07-15 …
平行四边形作图题如图形如平行四边形ABCD的土地中,有一条小路E-G-F,E在边AB上,F在CD上. 2020-11-06 …
如图,在边长为a的正方形ABCD中,E为AB边上的动点,F为BC边上的动点,△BEF的周长是2a.如 2020-12-03 …
在菱形ABCD中AB=4,在菱形ABCD中,AB=4,∠BAD等于θ,△AEF为正三角形,E,F在菱 2020-12-23 …