早教吧作业答案频道 -->数学-->
(1)尺规作图:如图a,已知∠MON,作∠MON的平分线OP,并在OP上任取一点Q,分别在OM、ON上各取一点S、T,作△OSQ和△OTQ,使得△OSQ≌△OTQ.(不写作法,保留作图痕迹)(2)请你参考这个
题目详情
(1)尺规作图:如图a,已知∠MON,作∠MON的平分线OP,并在OP上任取一点Q,分别在OM、ON上各取一点S、T,作△OSQ和△OTQ,使得△OSQ≌△OTQ.(不写作法,保留作图痕迹)
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图b,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
②如图c,在△ABC中,如果∠ACB不是直角,而①中的其它条件不变,请问,你在①中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
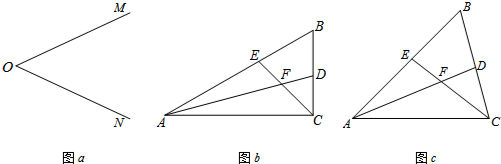
(2)请你参考这个作全等三角形的方法,解答下列问题:
①如图b,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
②如图c,在△ABC中,如果∠ACB不是直角,而①中的其它条件不变,请问,你在①中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

▼优质解答
答案和解析
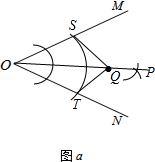 (1)如图a所示:
(1)如图a所示:
(2)①EF=DF,
如图b,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°-60°-90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=
(180°-60°)=60°,
在△AFC中,∠AFC=180°-(∠FAC+∠FCA)=180°-60°=120°,
∴∠EFD=∠AFC=120°,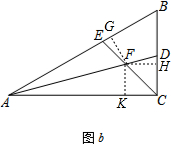
∴∠EFG=∠DFH,
在△EFG和△DFH中,
,
∴△EFG≌△DFH(ASA),
∴FE=FD.
EF=FD仍然成立.
②如图c,
过点F分别作FG⊥AB于点G,FH⊥BC于点H.
∴∠FGE=∠FHD=90°,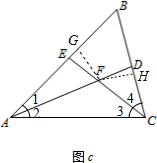
∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH(角平分线上的点到角的两边相等).
又∵∠HDF=∠B+∠1(外角的性质),
∴∠GEF=∠HDF.
在△EGF与△DHF中,
,
∴△EGF≌△DHF(AAS),
∴FE=FD.
 (1)如图a所示:
(1)如图a所示:(2)①EF=DF,
如图b,过点F作FG⊥AB于G,作FH⊥BC于H,作FK⊥AC于K,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴FG=FH=FK,
在四边形BGFH中,∠GFH=360°-60°-90°×2=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,∠B=60°,
∴∠FAC+∠FCA=
| 1 |
| 2 |
在△AFC中,∠AFC=180°-(∠FAC+∠FCA)=180°-60°=120°,
∴∠EFD=∠AFC=120°,

∴∠EFG=∠DFH,
在△EFG和△DFH中,
|
∴△EFG≌△DFH(ASA),
∴FE=FD.
EF=FD仍然成立.
②如图c,
过点F分别作FG⊥AB于点G,FH⊥BC于点H.
∴∠FGE=∠FHD=90°,

∵∠B=60°,且AD,CE分别是∠BAC,∠BCA的平分线,
∴∠2+∠3=60°,F是△ABC的内心,
∴∠GEF=∠BAC+∠3=60°+∠1,
∵F是△ABC的内心,即F在∠ABC的角平分线上,
∴FG=FH(角平分线上的点到角的两边相等).
又∵∠HDF=∠B+∠1(外角的性质),
∴∠GEF=∠HDF.
在△EGF与△DHF中,
|
∴△EGF≌△DHF(AAS),
∴FE=FD.
看了(1)尺规作图:如图a,已知∠...的网友还看了以下:
1道关于平面直角坐标系的题在平面直角坐标系中已知M(1,-3)N(-1,-4),试在直线y=x+1 2020-05-23 …
场源电荷Q=2乘10的副4次C是正点电荷检验电荷q=-2乘10的副5次C,是副点电荷他们相距r=2 2020-06-15 …
概率问题向正方形区域样本空间={(p,q)||p|≤1,|q|≤1}中随机投一点,如果(p,q)是 2020-06-22 …
在真空中O点放一个点电荷Q=1.0*10^-9.直线MN过点O,OM=30cm.M点放有一个点电荷 2020-06-30 …
在真空O点放一个点电荷Q=+1.0乘10负9次方库仑,直线MN通过O点,OM的距离r=30cm,M 2020-07-09 …
在平面直角坐标系xOy中,若P和Q两点关于原点对称,则称点P与点Q是一个“和谐点对”,表示为[P, 2020-07-30 …
已知点P和点Q是曲线y=x2-2x-3上的两点,且点P的横坐标是1,点Q的横坐标是4,求:已知点P 2020-07-31 …
电荷题目高手来啊!点电荷Q的电场中,将一电荷量q=2.0*10^-10c的点电荷放在与Q相距r=0 2020-08-01 …
如图1,点P,Q分别是边长为4CM的等边三角形ABC边AB,BC的动点,点P从顶点A,点Q从顶点B同 2020-11-04 …
,已知点P和点Q是曲线y=x^2-2x-3上的两点,且点P的横坐标是1,点Q的横坐标是4,求(1)知 2021-02-07 …