早教吧作业答案频道 -->数学-->
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.(1)求证:△ABP∽△PCF;(2)求∠ECF的度数;(3)若∠
题目详情
如图,在正方形ABCD中,点P是BC边上一点(不与B、C重合),连接PA,将线段PA绕点P顺时针旋转90°得到线段PE,交边DC于F,连接AE,CE.
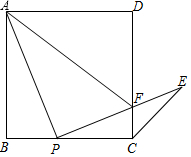
(1)求证:△ABP∽△PCF;
(2)求∠ECF的度数;
(3)若∠APB=75°,PC=2,求S△APE.

(1)求证:△ABP∽△PCF;
(2)求∠ECF的度数;
(3)若∠APB=75°,PC=2,求S△APE.
▼优质解答
答案和解析
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵∠APE=90°,
∴∠EPC+∠APB=90°,
∴∠PAB=∠EPC,
∴△ABP∽△PCF;
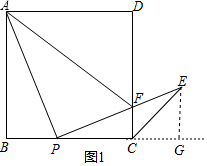
(2)如图1,过点E作EG⊥BC,垂足为G.
在△ABP和△PGE中,
.
∴△ABP≌△PGE,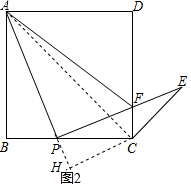
∴BP=EG,PG=AB,
∵AB=BC,
∴BC=PG,
∴BC-PC=PG-PC,即BP=CG,
∴CG=EG,
又∵∠EGC=90°,
∴∠ECG=45°,
∴∠ECF=45°;
(3)如图2,连接AC,过C作CH⊥AP交AP的延长线于H,
设PB=x,则AB=BC=x+2,
∴AC=
(x+2),
∵∠BAP=15°,∠BAC=45°,
∴∠PAC=30°,
∴CH=
AC=
,
∵∠B=∠H=90°,∠APB=∠CPH,
∴△ABP∽△CHP,
∴
=
,即
=
,
∴AP=2
,
∴S△APE=
×2
×2
=4.
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵∠APE=90°,
∴∠EPC+∠APB=90°,
∴∠PAB=∠EPC,
∴△ABP∽△PCF;
(2)如图1,过点E作EG⊥BC,垂足为G.
在△ABP和△PGE中,
|
∴△ABP≌△PGE,

∴BP=EG,PG=AB,
∵AB=BC,
∴BC=PG,
∴BC-PC=PG-PC,即BP=CG,
∴CG=EG,
又∵∠EGC=90°,
∴∠ECG=45°,
∴∠ECF=45°;
(3)如图2,连接AC,过C作CH⊥AP交AP的延长线于H,
设PB=x,则AB=BC=x+2,
∴AC=
| 2 |
∵∠BAP=15°,∠BAC=45°,
∴∠PAC=30°,
∴CH=
| 1 |
| 2 |
| ||
| 2 |
∵∠B=∠H=90°,∠APB=∠CPH,
∴△ABP∽△CHP,
∴
| CH |
| AB |
| PC |
| AP |
| ||||
| x+2 |
| 2 |
| AP |
∴AP=2
| 2 |
∴S△APE=
| 1 |
| 2 |
| 2 |
| 2 |
看了如图,在正方形ABCD中,点P...的网友还看了以下:
已知集合A={x|x2-2x-15≤0},B=(2,11],C=[p+1,2p-1],C≠∅.(1 2020-05-13 …
求三角形内切圆半径的公式r=[(p-a)(p-b)(p-c)/p]^(1/2),a、b、c为三角形 2020-05-20 …
不定积分dp/((1+p^2)^3/2)的答案带不带负号?我是按照三角替换做的,p=tant原式= 2020-07-11 …
谁能帮我证明海轮公式一个三角形,三边长a,b,c,p=1/2*(a+b+c),求三角形面积?面积s 2020-07-15 …
已知向量组α1,α2,α3线性无关,问:参数a,b,c满足什么条件时,向量组aα1+α2,bα2+ 2020-07-21 …
设向量组α1,α2,α3线性无关,问常数a,b,c满足什么条件aα1-α2,bα2-α3,cα3- 2020-07-21 …
(*p)[3]在里面是什么意思,另外定义一个数组吗*题9.66C若有以下定义和语句,则对a数组元素 2020-08-03 …
我要配置一种染色剂,但是总是不成功,氯化铝溶液(200C,p=1.16g/mL):六水合氯化铝(AI 2020-11-24 …
.单选题:若有以下说明和语句,C语言intc[4][5],(*p)[5];p=c;能正确引用c数组元 2020-12-13 …
已知三角形ABC三边长为a、b、c,p=1/2(a+b+c),S为面积,Ra为角A所对的旁切圆的半径 2021-02-07 …