早教吧作业答案频道 -->数学-->
已知点M(-1,0),N(1,0),曲线E上任意一点到M的距离均是到点N距离的3倍.(1)求曲线E的方程;(2)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点,C
题目详情
已知点M(-1,0),N(1,0),曲线E上任意一点到M的距离均是到点N距离的
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点,C,D两点均在x轴下方,求四边形ABCD面积的最大值.
| 3 |
(1)求曲线E的方程;
(2)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点,C,D两点均在x轴下方,求四边形ABCD面积的最大值.
▼优质解答
答案和解析
(1)设曲线E上任意一点坐标为(x,y),
由题意,
=
•
,-----(2分)
整理得x2+y2-4x+1=0,即(x-2)2+y2=3为所求.--…(5分)
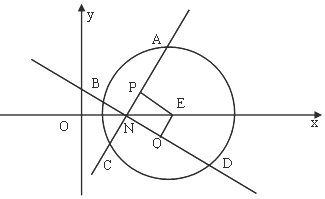
(2)由题意可知l1⊥l2,且两条直线均恒过点N(1,0)…(7分)
则四边形的面积:S=
AC•BD…(8分)
取AC的中点P,BD的中点Q,连结EP、EQ,
EP2=3-
AC2,EQ2=3-
BD2,
又可知四边形NPEQ为矩形,所以有EP2+EQ2=EN2=4
整理得:AC2+BD2=8…(10分)
故S=
AC•BD≤
•
=2
当AC=BD,即m=1时,即面积最大值为2…(12分)
由题意,
| (x+1)2+y2 |
| 3 |
| (x-1)2+y2 |
整理得x2+y2-4x+1=0,即(x-2)2+y2=3为所求.--…(5分)
(2)由题意可知l1⊥l2,且两条直线均恒过点N(1,0)…(7分)
则四边形的面积:S=
| 1 |
| 2 |
取AC的中点P,BD的中点Q,连结EP、EQ,
EP2=3-
| 1 |
| 4 |
| 1 |
| 4 |
又可知四边形NPEQ为矩形,所以有EP2+EQ2=EN2=4
整理得:AC2+BD2=8…(10分)
故S=
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BD2 |
| 2 |
当AC=BD,即m=1时,即面积最大值为2…(12分)

看了已知点M(-1,0),N(1,...的网友还看了以下:
已知M={m,n,p,q},其中m,n为关于x的方程x^2-ax+b=0的两个根,p,q为关于y的 2020-05-13 …
matlab求解三元回归方程.请把代码贴出来看下其中α,β,γ为未知数; 其他的有多组数据,这个方 2020-05-16 …
在任命工程督导时,对非合作王程,~般升级改造工程由()任命工程督导,重大升级改造工程由()任命工程督 2020-05-31 …
任选一个数后怎样运算得5201314我以前看过一个有趣得运算,就是任选一个数字,经过加减乘除的一系 2020-07-07 …
在平面直角坐标系中,已知x轴上的两点A(x1,0)B(x2,0)的距离记做|AB|=|X1-X2| 2020-07-30 …
已知点A(4,0)和圆:x2+y2=4(圆心在原点,半径为2),点P是圆O上任意一点,M是PA的中 2020-07-31 …
线性代数,关于齐次线性方程组通解例如一个方程组,5个未知数,只有3个方程,变换之后矩阵A的秩为3, 2020-08-02 …
一道数学题!某种考试有10道判断题,若有一个对题目毫无所知的人,对10道题任意猜测,其猜对6题的概率 2020-11-06 …
物理题···在声音的感知过程中,任何部分发生障碍,人都可以失去听觉,但只是传导障碍,人们可以通过其他 2020-11-27 …
探月工程与载人航天的关系要知道二者都是烧钱的主(我不是反对任何一个,相反其中任何一项成果我都由衷高兴 2021-02-02 …