早教吧作业答案频道 -->数学-->
如图,点P是正方形ABCD内一点,PA=1,PB=22,PD=10,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求PP′的长;(2)求∠BPQ的大小.
题目详情
如图,点P是正方形ABCD内一点,PA=1,PB=2
,PD=
,将△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
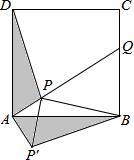
(1)求PP′的长;
(2)求∠BPQ的大小.
| 2 |
| 10 |

(1)求PP′的长;
(2)求∠BPQ的大小.
▼优质解答
答案和解析
(1)∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′=1,PD=P′B=
,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形,
∴PP′=
=
;
(2)∵△APP′是等腰直角三角形,
∴∠APP′=45°,
在△PP′B中,PP′=
,PB=2
,P′B=
,
∵(
)2+(2
)2=(
)2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°-∠APP′-∠P′PB=180°-45°-90°=45°.
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′=1,PD=P′B=
| 10 |
∴△APP′是等腰直角三角形,
∴PP′=
| PA2+P′A2 |
| 2 |
(2)∵△APP′是等腰直角三角形,
∴∠APP′=45°,
在△PP′B中,PP′=
| 2 |
| 2 |
| 10 |
∵(
| 2 |
| 2 |
| 10 |
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°-∠APP′-∠P′PB=180°-45°-90°=45°.
看了如图,点P是正方形ABCD内一...的网友还看了以下:
四棱锥P-ABCD的底面ABCD为边长1的菱形,角BCD=60,E是CD中点,PA垂直底面ABCD 2020-05-16 …
关于语言的几道题18.已知int a,*p=&a;则函数调用中错误的是().A) scanf(“% 2020-05-17 …
如图,A,B,C,D,P是⊙O上的五个点,且∠APB=∠CPD1.A,B,C,D,P是⊙O上的五个 2020-05-20 …
已知:如图,直线y=x-1交x轴、y轴于点A、B.直线y=-0.5x+2交x轴、y轴于点C、D,两 2020-05-23 …
英语翻译于是A公司在A银行的配合下,聘请了当地较有声望的律师对代收行B银行,因其将D/P远期作为D 2020-05-24 …
(47)A.I帧B.S帧C.B帧D.P帧 2020-05-26 …
设A,B为任意两个事件且A⊂B,P(B)>0,则下列选项必然成立的是()A.P(A)<P(A|B) 2020-06-18 …
概率论,对于任意A,B,下面结论正确的是对于任意A,B,下面结论正确的是()A.若P(AB)=0, 2020-07-30 …
判断点是否在平面上已知空间一平面上的5个点:A,B,C,D,P;怎样判断点P是否在A,B,C,D组 2020-07-31 …
设A,B为两个互斥事件,且P(A)>0,P(B)>0,则下列正确的是()A.P(A|B)=P(A)B 2020-12-01 …