早教吧作业答案频道 -->数学-->
在平面直角坐标系中,O为原点,点A(-4,0),点B(0,4),将△ABO)绕点O顺时针旋转,得△A′B′O,记旋转角为α,直线AA′与直线BB′相交于点P.(Ⅰ)如图①,当0°<α<90°时,求证
题目详情
在平面直角坐标系中,O为原点,点A(-4,0),点B(0,4),将△ABO)绕点O顺时针旋转,得△A′B′O,记旋转角为α,直线AA′与直线BB′相交于点P.
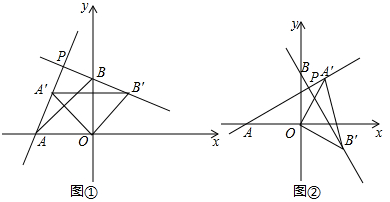
(Ⅰ)如图①,当0°<α<90°时,求证:AP⊥BP;
(Ⅱ)如图②,当90°<α<180°时,求证:AP⊥BP;
(Ⅲ)求点P的纵坐标的最大值与最小值(直接写出结果即可).
(Ⅰ)如图①,当0°<α<90°时,求证:AP⊥BP;
(Ⅱ)如图②,当90°<α<180°时,求证:AP⊥BP;
(Ⅲ)求点P的纵坐标的最大值与最小值(直接写出结果即可).

▼优质解答
答案和解析
 (Ⅰ)如图①,∵点A(-4,0),点B(0,4),
(Ⅰ)如图①,∵点A(-4,0),点B(0,4),
∴OA=OB=4,
∵△ABO绕点O顺时针旋转,得△A′B′O,
∴OA=OA′=OB=OB′,∠AOA′=∠BOB′=α,∠A′OB′=∠AOB=90°,
∴∠OA′A=∠OB′B=
(180°-α)=90°-
α,
∵∠OA′P+∠OA′A=180°,
∴∠OB′B+∠OA′P=180°,
在四边形OA′PB中,∵∠A′PB+∠A′OB′+∠OB′B+∠OA′P=360°,
∴∠A′PB+∠A′OB′=180°,
∴∠A′PB=90°,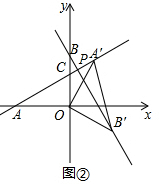
∴AP⊥BP;
(Ⅱ)如图②,
由(Ⅰ)得∴∠OAA′=∠OBB′=
(180°-α)=90°-
α,
在△AOC和△BCP中,∵∠ACO=∠BCP,
∴∠AOC=∠CPB=90°,
∴AP⊥BP;
(Ⅲ)∵∠BPA=90°,
∴点P在以AB为直径的圆上,
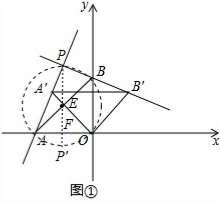
取AB的中点E,过点E作直径PP′⊥x轴交x轴于F点,如图①,此时P点的纵坐标最大,点P′的纵坐标最小,
∵△ABC为等腰直角三角形,
∴AB=4
,
∴EP=EP′=2
,
∵EF⊥OA,
∴EF=
OA=2,
∴FP=2
+2,FP′=2
-2,
∴P点的纵坐标为2+2
,点P′的纵坐标为2-2
,
即点P的纵坐标的最大值为2+2
,最小值为2-2
.
 (Ⅰ)如图①,∵点A(-4,0),点B(0,4),
(Ⅰ)如图①,∵点A(-4,0),点B(0,4),∴OA=OB=4,
∵△ABO绕点O顺时针旋转,得△A′B′O,
∴OA=OA′=OB=OB′,∠AOA′=∠BOB′=α,∠A′OB′=∠AOB=90°,
∴∠OA′A=∠OB′B=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OA′P+∠OA′A=180°,
∴∠OB′B+∠OA′P=180°,
在四边形OA′PB中,∵∠A′PB+∠A′OB′+∠OB′B+∠OA′P=360°,
∴∠A′PB+∠A′OB′=180°,
∴∠A′PB=90°,

∴AP⊥BP;
(Ⅱ)如图②,
由(Ⅰ)得∴∠OAA′=∠OBB′=
| 1 |
| 2 |
| 1 |
| 2 |
在△AOC和△BCP中,∵∠ACO=∠BCP,
∴∠AOC=∠CPB=90°,
∴AP⊥BP;
(Ⅲ)∵∠BPA=90°,
∴点P在以AB为直径的圆上,
取AB的中点E,过点E作直径PP′⊥x轴交x轴于F点,如图①,此时P点的纵坐标最大,点P′的纵坐标最小,
∵△ABC为等腰直角三角形,
∴AB=4
| 2 |
∴EP=EP′=2
| 2 |
∵EF⊥OA,
∴EF=
| 1 |
| 2 |
∴FP=2
| 2 |
| 2 |
∴P点的纵坐标为2+2
| 2 |
| 2 |
即点P的纵坐标的最大值为2+2
| 2 |
| 2 |
看了在平面直角坐标系中,O为原点,...的网友还看了以下:
将Rt三角形绕点A逆时针旋转90度得到三角形ADF,BC的延长线交DF于点E,连接BD.已知BC= 2020-04-25 …
已知如图P为正方形ABCD内一点,△ABP绕点B顺时针现在旋转得到三角形CBE,求证三角形BPE是 2020-05-16 …
1道求边长的计算题1道证明线段相等的证明题1道证明线段平行的证明题1道证明线段垂直的的证明题1道证 2020-06-03 …
全等三角形的数学题1.AB=AC.BD=CE/角B=角C.证明:AD=AE2.AB//CD.点C是 2020-06-27 …
如图在rt三角形abc中角acb等于九十度点df分别在abac上cf等于cb连接CD,将线段c绕点 2020-07-18 …
(三角形)已知P为等边三角形ABC内的一点,角BPC=110度,角BPA=x度,将三角形APB绕A 2020-07-23 …
求证:角α为第二或第三象限角当且仅当sinα·tanα<0求证:角θ为第一或第四象限角当且仅当(s 2020-07-23 …
勾股定理超难的题十级以上再进吧!将直角三角形ABC绕直角顶点C旋转,使点A落在BC边上的A',利用 2020-07-29 …
有关平面几何的数学题M为三角形ABC内一点,AB=AC,已知角AMB大于角AMC,求证:角BAM小 2020-08-02 …
求证直角三角形中30度所对角为斜边的一半不可以逆向判定直角三角形已知一个三角形中,有一个角为30度, 2020-12-15 …