早教吧作业答案频道 -->数学-->
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=5,B,C分别为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.(1)求证:AB∥FG;(2)求正四棱锥P-AMDE的外接球的
题目详情
如图,在正四棱锥P-AMDE,底面AMDE的边长为2,侧棱PA=
,B,C分别
为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.
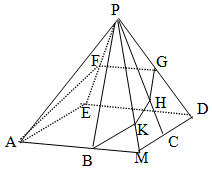
(1)求证:AB∥FG;
(2)求正四棱锥P-AMDE的外接球的表面积.
| 5 |
为AM,MD的中点.F为棱PE的中点,平面ABF与棱PD,PC,PM分别交于点G,H,K.

(1)求证:AB∥FG;
(2)求正四棱锥P-AMDE的外接球的表面积.
▼优质解答
答案和解析
(1)证明:在正方形AMDE中,因为B是AM的中点,所以AB∥DE.
又因为AB⊄平面PDE,DE⊂平面PDE
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2) 连接AD,EM,相交于O′,易得AO′=
,PO′=
.
由正四棱锥P-AMDE的对称性,
得正四棱锥P-AMDE得外接球球心在线段PO′上,
不妨设为O点.设OA=OP=R,则OO′=
-R,
∵AO2=AO′2+OO′2,
∴R2=2+(
-R)2,
∴R=
∴S=4πR2=
,
∴正四棱锥P-AMDE的外接球的表面积为
.
又因为AB⊄平面PDE,DE⊂平面PDE
所以AB∥平面PDE.
因为AB⊂平面ABF,且平面ABF∩平面PDE=FG,
所以AB∥FG.
(2) 连接AD,EM,相交于O′,易得AO′=
| 2 |
| 3 |
由正四棱锥P-AMDE的对称性,
得正四棱锥P-AMDE得外接球球心在线段PO′上,
不妨设为O点.设OA=OP=R,则OO′=
| 3 |
∵AO2=AO′2+OO′2,
∴R2=2+(
| 3 |
∴R=
5
| ||
| 6 |
∴S=4πR2=
| 25π |
| 3 |
∴正四棱锥P-AMDE的外接球的表面积为
| 25π |
| 3 |
看了如图,在正四棱锥P-AMDE,...的网友还看了以下:
在平行四边形ABCD中,E、F、G、H分别为四边上的点,且AE:EB=BF:FC=CG:GD=DH 2020-05-13 …
杂化轨道理论问题拿Nh3做例子吧,明明N原子2P轨道有3个未成对电子,可以达到结合3个H原子的条件 2020-05-13 …
某客户安装三相四线有功表的常数为2000r/KW.h,TA变比为150/5A.用秒表法测得圆盘转1 2020-05-13 …
变限积分求道问题对函数f(t+h)-f(t-h)在[-h,h]上的积分对h求导.F(h)=∫[-h 2020-05-23 …
A、B、C、D、E、F、G、H共八人为四对夫妻.已知:(一)E曾作客人参加了D的结婚典礼.(二)A 2020-06-16 …
肥达实验,如何讨论实验结果?伤寒0为全阴性,伤寒H为四个+,四个+,三个+,三个+,两个+,两个+ 2020-07-22 …
三角形的面积,a,b,c为三角形的边长,r为三角形内切圆的半径,利用类比推理,可得出四面体的体积为 2020-07-23 …
如图,E、F、G、H分别为四边形ABCD四边之中点.(1)求证:四边形EFGH为平行四边形;(2) 2020-07-30 …
如图,H为四棱锥P-ABCD的棱PC的三等分点,且PH=12HC,点G在AH上,AG=mAH.四边 2020-07-31 …
A、B、C、D、E、F、G、H共八人为四对夫妻。已知:(一)E曾作客人参加了D的结婚典礼。(二)A的 2020-11-02 …