早教吧作业答案频道 -->数学-->
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=12BC=2,M是EC的中点.(1)求证:DM∥平面ABE;(2)求三棱锥M-BDE的体积.
题目详情
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=
BC=2,M是EC的中点.
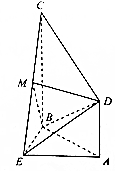
(1)求证:DM∥平面ABE;
(2)求三棱锥M-BDE的体积.
| 1 |
| 2 |

(1)求证:DM∥平面ABE;
(2)求三棱锥M-BDE的体积.
▼优质解答
答案和解析
 (满分12分)
(满分12分)
证明:(I)方法一:取BE的中点O,
连接OA、OM,…(1分)
因为O、M分别为线段BE、CE的中点,
所以OM=
BC …(2分)
又因为AD=
BC,所以OM=AD …(3分)
所以四边形OMDA为平行四边形,
所以DM∥AO,…(4分)
又因为AO⊂面ABE,MD⊄面ABE,所以DM∥平面ABE; …(6分)
方法二:取BC的中点N,连接DN、MN,…(1分)
因为M、N分别为线段CE、BC的中点,所以MN∥BE…(2分)
又因为BM⊂面ABE,MN⊄面ABE,所以MN∥平面ABE,…(3分)
同理可证DN∥平面ABE,…(4分)
MN∩DN=N,所以平面DMN∥平面ABE,…(5分)
又因为DM⊂面DMN,所以DM∥平面ABE…(6分)
(II)方法一:接(1)的方法一
因为平面ABE∩底面ABCD=AB
又因为平面ABE⊥底面ABCD,AB⊥BC
且BC⊂平面ABCD,
所以BC⊥底面ABE,…(7分)
OA⊂平面ABE,所以BC⊥AO…(8分)
又BE⊥AO,BC∩BE=B,
所以AO⊥平面BCE…(9分)
由(1)知DM=AO=
,DM∥AO,
所以DM⊥平面BCE …(10分)
VM-BDE=VD-MBE=
×
×2×2×
=
…(12分)
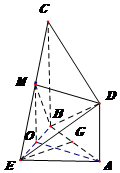
方法二:取AB的中点G,连接EG,
因为△ABE是等边三角形,所以EG⊥AB…(7分)
又因为平面ABE∩底面ABCD=AB
又因为平面ABE⊥底面ABCD,且EG⊂平面PAB,
所以EG⊥底面ABCD,即EG为四棱锥P-ABCD的高…(8分)
因为M是EC的中点,所以M-BCD的体积是E-BCD体积的一半,
所以计算三棱锥M-BDE的体积即计算三棱锥E-BDC体积减去三棱锥M-BDC的体积…(10分)
所以VM-BDE=
×
×
×2×4×
=
即三棱锥M-BDE的体积为
…(12分)
 (满分12分)
(满分12分)证明:(I)方法一:取BE的中点O,
连接OA、OM,…(1分)
因为O、M分别为线段BE、CE的中点,
所以OM=
| 1 |
| 2 |
又因为AD=
| 1 |
| 2 |
所以四边形OMDA为平行四边形,
所以DM∥AO,…(4分)
又因为AO⊂面ABE,MD⊄面ABE,所以DM∥平面ABE; …(6分)
方法二:取BC的中点N,连接DN、MN,…(1分)
因为M、N分别为线段CE、BC的中点,所以MN∥BE…(2分)
又因为BM⊂面ABE,MN⊄面ABE,所以MN∥平面ABE,…(3分)
同理可证DN∥平面ABE,…(4分)
MN∩DN=N,所以平面DMN∥平面ABE,…(5分)
又因为DM⊂面DMN,所以DM∥平面ABE…(6分)
(II)方法一:接(1)的方法一
因为平面ABE∩底面ABCD=AB
又因为平面ABE⊥底面ABCD,AB⊥BC
且BC⊂平面ABCD,
所以BC⊥底面ABE,…(7分)
OA⊂平面ABE,所以BC⊥AO…(8分)
又BE⊥AO,BC∩BE=B,
所以AO⊥平面BCE…(9分)
由(1)知DM=AO=
| 3 |
所以DM⊥平面BCE …(10分)
VM-BDE=VD-MBE=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
方法二:取AB的中点G,连接EG,
因为△ABE是等边三角形,所以EG⊥AB…(7分)
又因为平面ABE∩底面ABCD=AB
又因为平面ABE⊥底面ABCD,且EG⊂平面PAB,
所以EG⊥底面ABCD,即EG为四棱锥P-ABCD的高…(8分)
因为M是EC的中点,所以M-BCD的体积是E-BCD体积的一半,
所以计算三棱锥M-BDE的体积即计算三棱锥E-BDC体积减去三棱锥M-BDC的体积…(10分)
所以VM-BDE=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
2
| ||
| 3 |
即三棱锥M-BDE的体积为
2
| ||
| 3 |
看了如图,在多面体ABCDE中,平...的网友还看了以下:
代数题、求高手解已知关于(m平方-1)x平方-3(3m-1)x+18=0有两个正整数根.△ABC的 2020-05-21 …
m的平方(m-1)-4(1-m)的平方(2x+3y)的平方-(3x-2y)的平方(a+b+c+d) 2020-05-23 …
已知直线L垂直平面A,直线M属于平面B下面有几个命题正确的是?1.A平行B推出L垂直M2.A垂直B 2020-06-02 …
如图,点A(m,m+1),B(m+3,m-1)都在反比例函数y=kx的图象上.(1)求m,k的值; 2020-06-11 …
如图所示,M为放在水平地面上的劈形物体,物块m在其斜面上受到沿斜面向上的力F作用,m与M都保持静止 2020-06-28 …
5分一道……X都是未知数吖,没有乘的1、设关于X的二次方程(m-1)x平方+(2m-4)x+m=0 2020-07-14 …
若m与三分之n互为相反数,则3m+()=01.若x=m,y=m,则x,y的关系是2.若xy=-1, 2020-07-17 …
质量分别为M和m的物块形状大小均相同,将它们通过轻绳和光滑定滑轮连接,如图甲所示,绳子在各处均平行 2020-07-20 …
都是一些化简分式的题了,今晚就要,“/”这个符号就是分数线、①m-n/m平方-n的平方=()/m+ 2020-07-30 …
高中数学题设复数z=(m-1)+(m平方-4m-5)i和复平面内的点Z对应,若点Z的位置分别满足下 2020-08-01 …