早教吧作业答案频道 -->数学-->
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:当E点旋转到CB的延长线上时(如图2
题目详情
已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转.
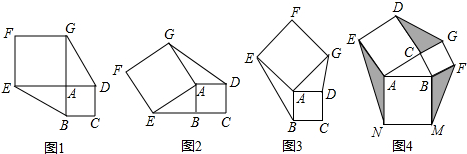
(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:___
当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:___
(2)引申与运用:当正方形AEFG旋转任意一个角度时(如图3),△ABE与△ADG的面积关系是___
并证明.
运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是___cm2.

(1)发现与证明:当E点旋转到DA的延长线上时(如图1),△ABE与△ADG的面积关系是:___
当E点旋转到CB的延长线上时(如图2),△ABE与△ADG的面积关系是:___
(2)引申与运用:当正方形AEFG旋转任意一个角度时(如图3),△ABE与△ADG的面积关系是___
并证明.
运用:已知△ABC,AB=5cm,BC=3cm,分别以AB、BC、CA为边向外作正方形(如图4),则图中阴影部分的面积和的最大值是___cm2.
▼优质解答
答案和解析
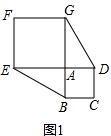 (1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
∴AE=AG,AB=AD,∠EAB=∠GAD,
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,如图2,
∴∠AHG=90°,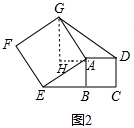
∵E点旋转到CB的延长线上,
∴∠ABE=90°,∠HAB=90°,
∴∠GAH=∠EAB,
在△AHG和△AEB中
,
∴△AHG≌△AEB,
∴GH=BE,
∵△ABE的面积=
EB•AB,△ADG的面积=
GH•AD,
∴△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,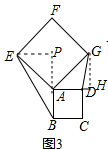
∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中
,
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABP的面积=
EP•AB,△ADG的面积=
GH•AD,
∴△ABP的面积=△ADG的面积;
运用:∵AB=5cm,BC=3cm,
∴AC=
=4cm,
∴△ABC的面积=
×3×4=6(cm2);
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.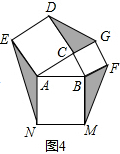
故答案为相等;相等;相等;18.
 (1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,
(1)①∵正方形ABCD和正方形AEFG有公顶点A,将正方形AEFG绕点A旋转,E点旋转到DA的延长线上,∴AE=AG,AB=AD,∠EAB=∠GAD,
∴△ABE≌△ADG(SAS),
∴△ABE的面积=△ADG的面积;
②作GH⊥DA交DA的延长线于H,如图2,
∴∠AHG=90°,

∵E点旋转到CB的延长线上,
∴∠ABE=90°,∠HAB=90°,
∴∠GAH=∠EAB,
在△AHG和△AEB中
|
∴△AHG≌△AEB,
∴GH=BE,
∵△ABE的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABE的面积=△ADG的面积;
(2)结论仍然成立.理由如下:
作GH⊥DA交DA的延长线于H,EP⊥BA交BA的延长线于P,如图3,

∵∠PAD=90°,∠EAG=90°,
∴∠PAE=∠GAH,
在△AHG和△AEP中
|
∴△AHG≌△AEP(AAS),
∴GH=BP,
∵△ABP的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴△ABP的面积=△ADG的面积;
运用:∵AB=5cm,BC=3cm,
∴AC=
| AB2-BC2 |
∴△ABC的面积=
| 1 |
| 2 |
根据(2)中的结论得到阴影部分的面积和的最大值=△ABC的面积的3倍=18cm2.

故答案为相等;相等;相等;18.
看了已知正方形ABCD和正方形AE...的网友还看了以下:
把正方形ABCD绕着点A,按顺时针方向旋转等到正方形AEFG,边FG与BC交于点H,试问线段HG与 2020-05-16 …
将正方形ABCD绕中心O顺时针旋转角α得到正方形A1B1C1D1.如图1所示.(1)当α=45°时 2020-05-16 …
将边长为3的正方形abcd绕点c按顺时针方向旋转30度边长为3的正方形ABCD绕点C按顺时针方向旋 2020-05-16 …
保证网络安全是使网络得到正常运行的保障,以下()说法是错误的。A.绕过防火墙,私自和外部网络连接, 2020-05-24 …
正方形ABCD绕点A旋转n度后得到正方形AEFG,EF与CD交于点O.1.连接DE,AO,证DE垂 2020-06-06 …
如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线 2020-06-20 …
把正△ABO绕着点O,按顺时针方向旋转任意角度α得到△CDO,边CD与AB交于点H(如图).(1)线 2020-11-03 …
(2013•拱墅区一模)如图,正方形ABCD的边长为3,将正方形ABCD绕点A顺时针旋转角度α(0° 2020-11-10 …
已知∑Un(n为1到正无穷)为正项级数,且∑Un(n为1到正无穷)的平方收敛,证明∑Un/n也收敛已 2020-11-18 …
如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线A 2021-01-02 …