早教吧作业答案频道 -->数学-->
数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?经过思考,小明展示了一种正确的思路:如图2,延
题目详情
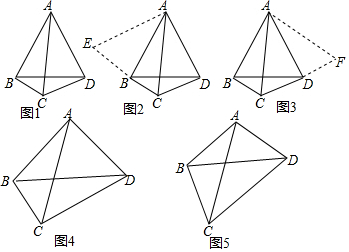
数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.
(2)小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.

▼优质解答
答案和解析
(1)BC+CD=
AC;
理由:如图1,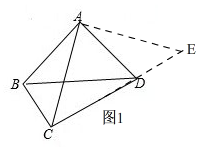
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=45°,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=90°,
∵∠ACB=∠ACD=45°,
∴∠ACB+∠ACD=45°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=45°,AC=AE,
∴△ACE是等腰直角三角形,
∴CE=
AC,
∵CE=CE+DE=CD+BC,
∴BC+CD=
AC;
(2)BC+CD=2AC•cosα.理由:如图2,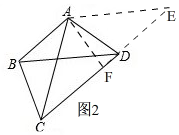
延长CD至E,使DE=BC,
∵∠ABD=∠ADB=α,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=180°-2α,
∵∠ACB=∠ACD=α,
∴∠ACB+∠ACD=2α,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=α,AC=AE,
∴∠AEC=α,
过点A作AF⊥CE于F,
∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,
∴CE=2CF=2AC•cosα,
∵CE=CD+DE=CD+BC,
∴BC+CD=2AC•cosα.
| 2 |
理由:如图1,

延长CD至E,使DE=BC,
∵∠ABD=∠ADB=45°,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=90°,
∵∠ACB=∠ACD=45°,
∴∠ACB+∠ACD=45°,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,
|
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=45°,AC=AE,
∴△ACE是等腰直角三角形,
∴CE=
| 2 |
∵CE=CE+DE=CD+BC,
∴BC+CD=
| 2 |
(2)BC+CD=2AC•cosα.理由:如图2,

延长CD至E,使DE=BC,
∵∠ABD=∠ADB=α,
∴AB=AD,∠BAD=180°-∠ABD-∠ADB=180°-2α,
∵∠ACB=∠ACD=α,
∴∠ACB+∠ACD=2α,
∴∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠ADE=180°,
∴∠ABC=∠ADE,
在△ABC和△ADE中,
|
∴△ABC≌△ADE(SAS),
∴∠ACB=∠AED=α,AC=AE,
∴∠AEC=α,
过点A作AF⊥CE于F,
∴CE=2CF,在Rt△ACF中,∠ACD=α,CF=AC•cos∠ACD=AC•cosα,
∴CE=2CF=2AC•cosα,
∵CE=CD+DE=CD+BC,
∴BC+CD=2AC•cosα.
看了数学课上,张老师出示了问题:如...的网友还看了以下:
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
下列有关地层和化石的叙述,正确的是A.在任何情况下,地层中下面的岩层总是比上面的岩层古老B.不论地 2020-06-19 …
令a、b、c是互不相等的正数如何证明aˆ2+1/aˆ2≥a+1/a成立令a、b、c是互不相等的正数 2020-07-09 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
不定积分变形a^x的导数为a^xlna.a^xlna*dx的原函数为不定积分∫(a^x/lna)+ 2020-08-02 …
绝对值不等式|x|≤a(a≥0)的解集可以如下获得:|x|≤a在数轴上的几何意义是“到原点距离不超 2020-08-03 …
关于平方根,下列说法正确的是()A.任何一个数有两个平方根,并且他们互为相反数B.负数没有平方根C. 2020-11-06 …
化学关于活化能若基元反应A-2B的活化能为Ea,而其逆活化能为Ea',问1.加催化剂后,其正、逆活化 2020-11-20 …
“不以规矩,难成方圆”这句古训,它所提示的道理是()A.做任何事都要有自信心B.有规矩才能画出方和圆 2020-11-24 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …